初中数学有理数无理数的概念与运算解答题

把几个数用大括号围起来，中间用逗号断开，如：{1，2，-3}、{−2，7，3 ,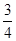，19}，我们称之为集合，其中的数称其为集合的元素．如果一个集合满足：当有理数a是集合的元素时，有理数10-a也必是这个集合的元素，这样的集合我们称为和谐集合．例如集合{2，8}，{-1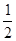，， ，11}就是两个和谐集合．
（1）请你判断集合{1，-10}，{-2，3.14，5，6.86，12}是不是和谐集合？
（2）请你写出满足条件的两个和谐集合的例子（至少有3个元素且不能与例题举例重复）；
（3）写出所有和谐集合中，元素个数最少的集合．

为增强市民的节水意识，某市对居民用水实行“阶梯收费”：规定每户每月不超过月用水标准部分的水价为1.5元/吨，超过月用水标准量部分的水价为2.5元/吨．该市小明家5月份用水12吨，交水费20元．请问：该市规定的每户月用水标准量是多少吨？

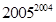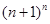（1）问题：你能比较和的大小吗？为了解决这个问题，首先写出它的一般形式，即比较和的大小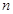（是正整数），然后我们从分析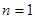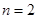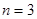，，，…这些简单情况入手，从中发现规律，经过归纳，猜想出结论.
通过计算，比较下列各组数的大小（在横线上填写“＞”、“＜”、“＝”号）：
，，，，，…
（2）从第（1）题的结果经过归纳，可以猜想出和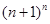的大小关系是什么？
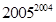（3）根据上面的归纳猜想，尝试比较和的大小.

有甲乙两个水桶，甲水桶里有1千克水，乙桶是空的，第一次将甲桶水里的二分之一倒入乙桶，第二次将乙桶里的三分之一倒入甲桶，第三次将甲桶的四分之一倒入乙桶，第四次又将乙桶的五分之一倒入甲桶．照这样来回倒下去，一直倒了2000次后，乙桶里有水多少千克？

如图甲，把一个边长为2的大正方形分成四个同样大小的小正方形，再连结大正方形的四边中点，得到了一个新的正方形（图中阴影部分），求:

（1）图甲中阴影部分的面积是多少？
（2）图甲中阴影部分正方形的边长是多少？
（3）如图乙，在数轴上以1个单位长度的线段为边作一个正方形，以表示数1的点为圆心，以正方形对角线长为半径画弧，交数轴负半轴于点A，求点A所表示的数是多少？

如图，数轴上有三个点A、B、C，它们可以沿着数轴左右移动，请回答：

（1）将点B向右移动三个单位长度后到达点D，点D表示的数是       ；
（2）移动点A到达点E，使B、C、E三点的其中任意一点为连接另外两点之间线段的中点，请你直接写出所有点A移动的距离和方向；
（3）若A、B、C三个点移动后得到三个互不相等的有理数，它们既可以表示为1，，的形式，又可以表示为0，，的形式，试求，的值.

有依次排列的3个数：3，9，8，对任相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，，8，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，，，9，8，继续依次操作下去，问：从数串3，9，8开始操作第一百次以后所产生的那个新数串的所有数之和是多少？

如图，边长分别为1，2，3，4，……，2007，2008的正 方形叠放在一起，请计算图中阴影部分的面积．

计算：＋（－1）²⁰¹³－（－2）^－2．

计算：

如图是一个“数值转换机”（箭头是指数进入转换机的路径,方框是对进入的数进行转换的转换机）。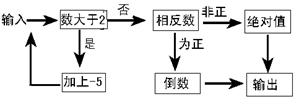

（1）、当小明输入4, 7, -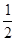 ,-2012 这四个数使,则四次输出的结果依次为       ,       ,       ,       。
（2）、你认为当输入数 等于            时（写出一个即可）,其输出结果为0。
（3）、你认为这个“数值转换机”不可能输出       数。
（4）、有一次,小明在操作的时候,输出的结果是2,聪明的你判断一下,小明输入的正整数是
          （用含自然数n的代数式表示）。

计算： ．

计算：

计算：

如图，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以看到终点表示的数是－2。

已知点A是数轴上的点，完成下列各题：
如果点A表示的数是3，将点A先向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________；
如果点A表示的数是－4，将点A先向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________；
一般地，如果点A表示的数是m，将点A先向右移动n个单位长度，再向左移动t个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________。