四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)试判断△AEF的形状,并说明理由;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,则四边形AECF的面积为 .(直接写结果)
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′′顺时针旋转90°,得到△A′′B′′C′′,请你画出△A′′B′′C′′和△A′′B′′C′′(不要求写画法).
如图,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,

(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2 ,则S1与S2的数量关系是 ;
(2)△ABF通过旋转可与△CDB重合,请指出旋转中心和最小旋转角的度数.
如图,不用量角器,在方格纸中画出△ABC绕点B顺时针方向旋转90°后得到的△A 1BC 1.

如图,已知在Rt△ABC中,∠ACB=90°,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F.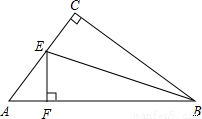
(1)求EF的长度;
(2)作CD⊥AB,垂足为D,CD与BE相交于G,试说明:CE=CG
如图,已知△ABC各顶点的坐标分别为A(-3,2),B(-4,-3),C(-1,-1),请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各点坐标.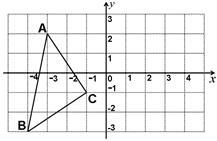
在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F.
(1)若点B的坐标是(-4,0),请在图中画出△AEF,并写出点E,F的坐标;
(2)点P为x轴上的一个动点,是否存在P使PA+PE的值最小?若不存在,请说明理由,若存在请求出点P的坐标.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.
(1)说明△A1B1C1是由△ABC经过怎样的平移得到的?
(2)直接写出点P2的坐标;
(3)计算△A1B1C1的面积.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.
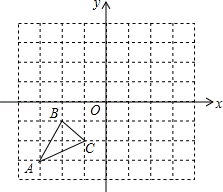
(1)请画出△ABC关于y轴对称的△A1B1C1;并写出B1点的坐标:
(2)若将△ABC顶点纵坐标都乘以-1,横坐标不变,得到的△A2B2C2与△ABC有怎样的位置关系: .
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).

(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
如图,在平面直角坐标系中,
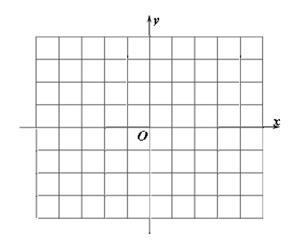
(1)描出A(- 4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是
(3)作出△ABC关于y轴的对称图形.
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗? 
操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
试题篮
()