已知线段AB,分别按下列要求画图(或作图),并保留痕迹.
(1)如图1,线段AB与A′B′关于某条直线对称,点A的对称点是A′,只用三角尺画出
点B的对称点B′;
(2)如图2,平移线段AB,使点A移到点A′的位置,用直尺和圆规作出点B的对应点
B′;
(3)如图3,线段AB绕点O顺时针方向旋转,其中OB=OA,点A旋转到点A′的位
置,只用圆规画出点B的对应点B′,并写出画法;
(7分)如图,正方形网格中,每一个小正方形的边长都是1,四边形ABCD的四
个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转180°.
试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)设点C旋转后的对应点为C′,则tan∠ AC′B= ▲ ;
AC′B= ▲ ;
(3) 求点C旋转过程中所经过的路径长.
(本题7分)如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.
⑴求∠DC E的度数;
E的度数;
⑵当AB=4,AD:DC="1:" 3时,求DE的长.
一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(α=∠BAD且0°<α<180°),使两块三角板至少有一组边平行。
(1)如图①,α=______°时,BC∥DE;
(2)请你分别在图②、图③的指定框内,各画一种符合要求的图形,标出α,并完成各项填空:
图②中α=______°时,______∥______;图③中α=______°时,______∥______。

(本题 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
,
(1)如图9,当 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交 边于点E,联结BE.
边于点E,联结BE.
①当 时,设
时,设 ,
, ,求
,求 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当 时,求
时,求 的长.
的长. 

如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连结AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然
成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.

如图,在平行四边形ABCD中,AB⊥AC,AB=1,BC= ,对角线AC、BD相交于点0,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F.
,对角线AC、BD相交于点0,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F.
(1)求证:当旋转角为90°时,四边形ABEF为平形四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由,并求出此时AC绕点0顺时针旋转的度数.
如图,在平面直角坐标系中,△ABC与△A1B1C1关于点E成中心对称
(1)画出对称中心E,并写出E、A、C的坐标;
(2)P(a,b)是△ABC的边上AC上一点,△ABC经平移后,点P的对应点是P2(A+6,B+2),请画出上述平移后的△A 2B2C2,并判断△A2B2C2与△A1B1C1的位置关系(直接写出结果).
2B2C2,并判断△A2B2C2与△A1B1C1的位置关系(直接写出结果).
如图,在3×3的正方形网格中,每个网格都有三个小正方形被涂黑.
(1)在图①中将一个空白部分的小正方形涂黑,使其余空白部分是轴对称图形但不是中心对称图形.
(2)在图②中将两个空白部分的小正方形涂黑,使其余空白部分是中心对称图形但不是轴对称图形.
.(10分)(1)如图1,已知点P在正三角形ABC的边BC上,以AP为边作正三角形APQ,连接CQ.
①求证:△ABP≌△ACQ;
②若AB=6,点D是AQ的中点,直接写出当点P由点B运动到点C时,点D运动路线的长.
(2)已知,△EFG中,EF=EG=13,FG=10.如图2,把△EFG绕点E旋转到△EF'G'的位置,点M是边EF'与边FG的交点,点N在边EG'上且EN=EM,连接GN.求点E到直线GN的距离.
已知两个全等的直角三角形纸片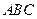 、
、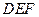 ,如图11放置,点
,如图11放置,点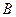 、
、 重合,点
重合,点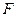 在
在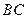 上,
上,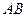 与
与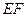 交于点
交于点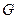 .
.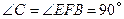 ,
, ,
,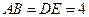 .
.
(1)求证: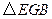 是等腰三角形;
是等腰三角形;
(2)若纸片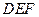 不动,若
不动,若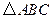 绕点
绕点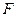 逆时针旋转.问首次使四边形
逆时针旋转.问首次使四边形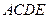 成为以
成为以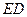 为底的梯形时,(如图12).旋转角α的度数是 度,并请你求出此时梯形的高.
为底的梯形时,(如图12).旋转角α的度数是 度,并请你求出此时梯形的高.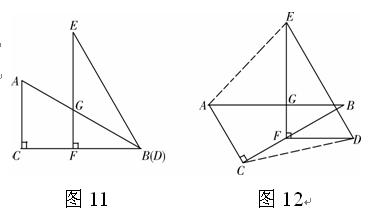
(本小题满分12分)你还记得图形的旋转吗?如图,P是正方形ABCD内一点,
PA=a,PB=2a,PC=3a.将△APB绕点B按顺时针方向旋转,使AB与BC重合,得△CBP,.
⑴ 求证:△PBP,是等腰直角三角形;
⑵ 猜想△PCP,的形状,并说明理由.
(本小题满分10分)已知,等腰Rt△ABC中,点O是斜边的中点,△MPN是直角三角形,固定△ABC,滑动△MPN,在滑动过程中始终保持点P在AC上,且PM⊥AB,PN⊥BC,垂足分别为E、F.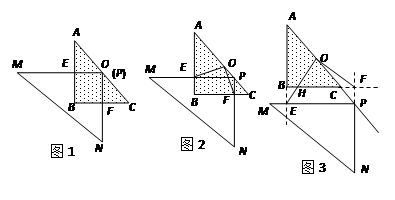
(1)如图1,当点P与点O重合时,OE、OF的数量和位置关系分别是____ __.
(2)当△MPN移动到图2的位置时,(1)中的结论还成立吗?请说明理由.
(3)如图3,等腰Rt△ABC的腰长为6,点P在AC的延长线上时,Rt△MPN的边 PM
与AB的延长线交于点E,直线BC与直线NP交于点F,OE交BC于点H,且 EH: HO=2:5,则BE的长是多少?
(本小题满分11分)
如图,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线
BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F与直线EN有怎样的位置关系?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系及点F与直线EN的位置关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.
△ABC在方格纸中的位置如图5所示,方格纸中的每个小正方形的边长为1个单位.
(1)△ 与△ABC关于纵轴(
与△ABC关于纵轴(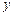 轴)对称,请你在图5中画出△
轴)对称,请你在图5中画出△ ;
;
(2)将△ABC向下平移8个单位后得到△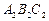 ,请你在图5中画出△
,请你在图5中画出△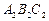 .
.
试题篮
()