某林场计划从外地购进两种小树苗2000棵进行栽培,已知甲种树苗每棵2元,乙种树苗每棵3元。
(1)若购买这批树苗共用4500元,求甲、乙两种树苗各购买了多少棵?
(2)若购买这批树苗的钱不超过4700元,问应选购甲种树苗至少多少棵?
(3)相关资料表明,甲、乙两种树苗的成活率分别是94%和99%,若要使这批树苗的成活率不低于96%,且树苗的总费用最少,问应选购甲、乙两种树苗各多少棵?总费用最少是多少元?
(1)计算:
(2)解方程组:
(3)解不等式组: .(将不等式组解集在数轴上表示出来)
.(将不等式组解集在数轴上表示出来)
购进某种干果,由于销售状况良好,超市又用9000元第二次购进该干果,但第二次的进价比第一次的提髙了20%,第二次购进干果数量是第一次的2倍还多300千克.
(1)求该干果的第一次进价是每千克多少元?
(2)百姓超市按每千克9元的价格出售,当大部分干果售出后,余下的按售价的8折售完,若两次销售这种干果的利润不少于5820元,则最多余下多少千克干果按售价的8折销售.
已知关于x的方程4x+2m+1=2x+5的解是负数.
(1)求m的取值范围;
(2)在(1)的条件下,解关于x的不等式2(x﹣2)>mx+3.
定义符号 的含义为:当
的含义为:当 时,
时, 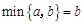 ;当
;当 时,
时,  .如:
.如: ,
, .
.
(1)求 ;
;
(2)已知 , 求实数
, 求实数 的取值范围;
的取值范围;
(3)当 时,
时, .直接写出实数
.直接写出实数 的取值范围.
的取值范围.
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表:

请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
我县某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
试题篮
()