如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为()
A.(-1,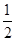 ) ) |
B.(0,0) | C.(-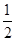 ,1) ,1) |
D.(-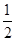 ,0) ,0) |
若二次函数的顶点坐标为(2,-1),且抛物线过(0,3),则二次函数的解析式是().
| A.y=-(x-2)2-1 |
| B.y=-(x-2)2-1 |
| C.y=(x-2)2-1 |
| D.y= -(x-2)2-1 |
一个小球被抛出后,如果距离地面的高度h(米)和运行时间t(秒)的函数解析式为h=-5t2+10t+1,那么小球到达最高点时距离地面的高度是()
| A.1米 | B.3米 | C.5米 | D.6米 |
在平面直角坐标系中,将抛物线y=x2-x-6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则|m|的最小值()
| A.1 | B.2 | C.3 | D.6 |
图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线 ,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为()
,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为()
A. 米 米 |
B. 米 米 |
C. 米 米 |
D. 米 米 |
乘雪橇沿倾斜角是 的斜坡滑下,滑下的路程S(米)与时间t(秒)间的关系式为
的斜坡滑下,滑下的路程S(米)与时间t(秒)间的关系式为 ,若滑到坡底的时间为2秒,则此人下滑的高度为()
,若滑到坡底的时间为2秒,则此人下滑的高度为()
| A.24米 | B.12米 | C. 米 米 |
D.6米 |
如图,已知二次函数 (
( )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③ ;
;
④ ;
;
其中正确的结论是()
| A.①③④ | B.①②③ | C.①②④ | D.①②③④ |
抛物线 经过平移得到抛物线
经过平移得到抛物线 ,平移方法是()
,平移方法是()
| A.向左平移1个单位,再向下平移2个单位 |
| B.向左平移1个单位,再向上平移2个单位 |
| C.向右平移1个单位,再向下平移2个单位 |
| D.向右平移1个单位,再向上平移2个单位 |
用配方法将二次函数y= x²-2x+1写成y=a(x-h)²+k的形式是()
x²-2x+1写成y=a(x-h)²+k的形式是()
A.y= (x-2)²-1 (x-2)²-1 |
B.y= (x-1)²-1 (x-1)²-1 |
C.y= (x-2)²-3 (x-2)²-3 |
D.y= (x-1)²-3 (x-1)²-3 |
抛物线y=3x2,y=-3x2,y= x2+3共有的性质是()
x2+3共有的性质是()
| A.开口向上 | B.对称轴是y轴 |
| C.都有最高点 | D.y随x值的增大而增大 |
关于抛物线y=(x-1)2-2,下列说法中错误的是
| A.顶点坐标为(1,-2) |
| B.对称轴是直线x=1 |
| C.当x>1时,y随x的增大而减小 |
| D.开口方向向上 |
抛物线y=x2+2x-1关于y轴对称的抛物线的解析式为 ()
| A.y=x2-2x-1 | B.y=x2-2x-3 |
| C.y=-x2+2x-3 | D.y=-x2-2x-1 |
二次函数y=ax2+bx+c的图象如图所示.现有下列4个判断:①ac<0; ②a+b=0;③4ac-b2=4a;④a+b+c<0,其中正确的有()
| A.1个 | B.2个 | C.3个 | D.4个 |
试题篮
()