初中数学二次函数在给定区间上的最值解答题

如图，有长为24米的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体（墙体的最大可用长度a=10米）：如果AB的长为x，面积为y，

（1）求面积y与x的函数关系（写出x的取值范围）
（2）x取何值时，面积最大？面积最大是多少？

二次函数y₁=a(x-2)²的图像与直线交于A（0，-1），B（2,0）两点。
（1）确定二次函数与直线AB的解析式。
（2）根据下图,分别确定当y₁<y₂，y₁=y₂，y₁>y₂时，自变量x的取值范围。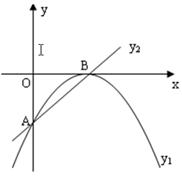

已知二次函数 .
（1）求二次函数与 轴的交点坐标；
（2）求二次函数的对称轴和顶点坐标；
（3）写出y随x增大而减小时自变量x的取值范围.

已知抛物线 ，
（1）用配方法确定它的顶点坐标、对称轴；
（2）取何值时，随增大而减小？
（3）取何值时，抛物线在轴上方？

（本题12分）为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．

采购数量（件）	1	2	…
A产品单价（元/件）	1480	1460	…
B产品单价（元/件）	1290	1280	…

 
（1）设A产品的采购数量为x（件），采购单价为y₁（元/件），求y₁与x的关系式；
（2）经商家与厂家协商，采购A产品的数量不少于B产品数量的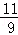，且A产品采购单价不低于1200元，求该商家共有几种进货方案；
（3）该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．

（本题本题10分）如图，在平面直角坐标系中，O是坐标原点，抛物线与轴正半轴交于点A，对称轴DE交轴于点E．点B在第二象限，过点B作BC⊥x轴于点C，连结AB，且AB=10，AC=8．将点B向右平移5个单位后，恰好与抛物线的顶点D重合．

（1）求点D的坐标；
（2）求该抛物线的解析式．

如图（1），抛物线与x轴交于A、B两点，与y轴交于点C（0，）．［图（2）为解答备用图］

（1）__________，点A的坐标为___________，点B的坐标为__________；
（2）设抛物线的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．

某商场销售一批名牌衬衣，平均每天可售出20件，每件衬衣盈利40元．为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衣降价1元，商场平均每天可多售出2件．
（1）若商场平均每天盈利1200元，每件衬衣应降价多少元？
（2）若要使商场平均每天的盈利最多，请你为商场设计降价方案．

若x₁、x₂是关于一元二次方程ax²+bx+c（a≠0）的两个根，则方程的两个根x₁、x₂和系数a、b、c有如下关系：x₁+x₂=-，x₁•x₂=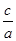．把它称为一元二次方程根与系数关系定理．如果设二次函数y=ax²+bx+c（a≠0）的图象与x轴的两个交点为A（x₁，0），B（x₂，0）．利用根与系数关系定理可以得到A、B两个交点间的距离为：AB=|x₁-x₂|=；
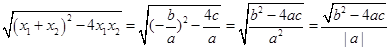参考以上定理和结论，解答下列问题：
设二次函数y=ax²+bx+c（a＞0）的图象与x轴的两个交点A（x₁，0），B（x₂，0），抛物线的顶点为C，显然△ABC为等腰三角形．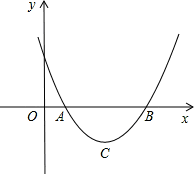

（1）当△ABC为直角三角形时，求b²-4ac的值；
（2）当△ABC为等边三角形时，求b²-4ac的值．

已知抛物线经过点A（3，0），B（－1，0）．
（1）求抛物线的解析式；
（2）求抛物线的顶点坐标．

（本题10分）抛物线y=-x²+（m-1）x+m与y轴交于（0，3）点． 
（1）求出m的值．
（2）求它与x轴的交点和抛物线顶点的坐标．
（3）x取值什么值时，抛物线在x轴上方？

传统节日“春节”到来之际，某商店老板以每件60元的价格购进一批商品，若以单价80元销售，每月可售出300件.调查表明：单价每上涨1元，该商品每月的销售量就减少10件。
（1）请写出每月销售该商品的利润y（元）与单价x（元）间的函数关系式；
（2）单价定为多少元时，每月销售商品的利润最大？最大利润为多少？

如图，二次函数y=ax²+bx+c的图象的顶点C的坐标为（0，-2），交x轴于A、B两点，其中A（-1，0），直线l：x=m（m＞1）与x轴交于D．

（1）求二次函数的解析式和B的坐标；
（2）在直线l上找点P（P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求点P的坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，在抛物线上是否存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形？如果存在，请求出点Q的坐标；如果不存在，请说明理由．

已知，如图，直线l经过A（4，0）和B（0，4）两点，它与抛物线y=ax²在第一象限内相交于点P，又知△AOP的面积为，求抛物线的函数表达式．

某商店将成本为30元的文化衫标价50元出售．
（1）为了搞促销活动经过两次降价调至每件40.5元，若两次降价的百分率相同，求每次降价的百分率；
（2）经调查，该文化衫每降5元，每月可多售出100件，若该品牌文化衫按原标价出售，每月可销售200件，那么销售价定为多少元，可以使该商店获得最大的利润？最大利润是多少?