初中数学二次函数在给定区间上的最值解答题

如图，在平面直角坐标系xOy中，将抛物线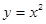的对称轴绕着点P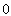（，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上的一点.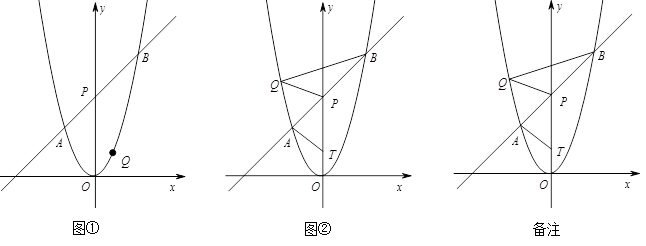

（1）求直线AB的函数表达式；
（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；
（3）如图②，若点Q在y轴左侧，且点T（0，t）（t<2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.

如图，已知抛物线（）的对称轴为直线，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

（1）若直线经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴上的一个动点，求使△BPC为直角三角形的点P的坐标．

已知抛物线E₁：y=x²经过点A（1，m），以原点为顶点的抛物线E₂经过点B（2，2），点A、B关于y 轴的对称点分别为点A′，B′．

（1）求m的值及抛物线E₂所表示的二次函数的表达式；
（2）如图1，在第一象限内，抛物线E₁上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；
（3）如图2，P为第一象限内的抛物线E₁上与点A不重合的一点，连接OP并延长与抛物线E₂相交于点P′，求△PAA′与△P′BB′的面积之比．

在平面直角坐标系中，抛物线与轴交于点，，与轴交于点，直线经过，两点．

（1）求抛物线的解析式；
（2）在上方的抛物线上有一动点．
①如图1，当点运动到某位置时，以为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点的坐标；21·cn·jy·com
②如图2，过点，的直线交于点，若，求的值．

如图，在矩形ABCD中，OA=5，AB=4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B恰好落在边OA上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．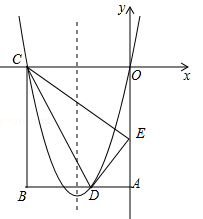

（1）求OE的长及经过O，D，C三点抛物线的解析式；
（2）一动点P从点C出发，沿CB以每秒2个单位长度的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长度的速度向点C运动，当点P到达点B时，两点同时停止运动，设运动时间为t秒，当t为何值时，DP=DQ；
（3）若点N在（1）中抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点坐标；若不存在，请说明理由．

如图，在平面直角坐标系 $xOy$中，直线 $y=\frac{1}{2}x+2$与 $x$轴交于点 $A$，与 $y$轴交于点 $C$．抛物线 $y=a{x}^2+bx+c$的对称轴是 $x=-\frac{3}{2}$且经过 $A$、 $C$两点，与 $x$轴的另一交点为点 $B$．

（1）①直接写出点 $B$的坐标；②求抛物线解析式．
（2）若点 $P$为直线 $AC$上方的抛物线上的一点，连接 $PA,PC$．求 $△PAC$的面积的最大值，并求出此时点 $P$的坐标．
（3）抛物线上是否存在点 $M$，过点 $M$作 $MN$垂直 $x$轴于点 $N$，使得以点 $A$、 $M$、 $N$为顶点的三角形与 $△ABC$相似？若存在，求出点 $M$的坐标；若不存在，请说明理由．

本题满分9分．
九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：

售价（元/件）	100	110	120	130	…
月销量（件）	200	180	160	140	…

 
已知该运动服的进价为每件60元，设售价为x元．
（1）请用含x的式子表示：
①销售该运动服每件的利润是    元；②月销量是    件；（直接填写结果）
（2）设销量该运动服的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？

如图，在平面直角坐标系中，抛物线经过点 $A（0，4），B（1，0），C（5，0）$，其对称轴与 $x$轴交于点 $M$．

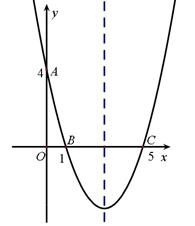
（1）求此抛物线的解析式和对称轴；
（2）在此抛物线的对称轴上是否存在一点 $P$，使 $△PAB$的周长最小？若存在，请求出点 $P$的坐标；若不存在，请说明理由；
（3）连接AC，在直线 $AC$下方的抛物线上，是否存在一点 $N$，使 $△NAC$的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．

设抛物线（）与x轴的交点为A（， 0），B（，0），且，其中，点P（a，b）为抛物线上一动点．

（1）求抛物线的解析式；
（2）连接AC，过P点做直线PE∥AC交x轴于点E，交y轴于点E（O，t），当a取何值时t有最大值，最大值是多少？
（3）判断在（2）的条件中是否存在一点P，使以点A、C、P、E为顶点的四边形为平行四边形．若不存在试说明理由；若存在，试求出点P的坐标．

如图，若二次函数的图像过点A（－1，0），C（0，），与x轴的另一交点为B，D为顶点．

（1）求m、n的值及B、D两点的坐标；
（2）若二次函数的图像的对称轴与x轴的交点为P，在线段BC上找一点Q，使得以点B、P、Q为顶点的三角形与△ABC相似，请求出所有符合条件的点Q坐标；
（3）将△ABC沿x轴向右平移t个单位长度（0<t<6），设平移后的△ABC与△PBD重叠的面积为S，请直接写出S 与t的函数关系式．

已知抛物线y=-x²-2x+a（a≠0）与y轴交于A，顶点为M，直线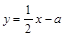分别与x轴、y轴交于B、C两点，并且与直线MA相交于N点。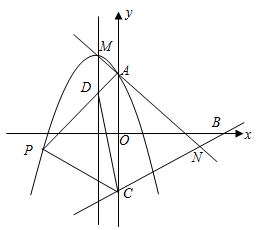

（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M、A的坐标；
（2）将△NAC沿着y轴翻折，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于D，连接CD。求a的值及△PCD的面积；
（3）在抛物线y=-x²-2x+a（a＞0）上是否存在点P，使得以P、A、C、N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由。

在平面直角坐标系xOy中，过点（0，2）且平行于x轴的直线，与直线y＝x－1交于点A，点A关于直线x＝1的对称点为B，抛物线C₁：y＝x²＋bx＋c经过点A，B.

（1）求点A，B的坐标；
（2）求抛物线C₁的表达式及顶点坐标；
（3）若拋物线C₂：y＝ax²（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围.

已知：如图，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．

（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果EF=2OG，求点Ｇ的坐标．
（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．

（本题8分）已知锐角△ABC中，边BC长为12，高AD长为8
（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K

①求的值
②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值
（2）若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．

如图，已知点O（0，0），A（－5，0），B（2，1），抛物线l：y＝－（x－h）²＋1（h为常数）与y轴的交点为C．

（1）l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标：
（2）设点C的级坐标为y_c，求y_c的最大值，此时l上有两点（x₁，y₁），（x₂，y₂），其中x₁＞x₂≥0，比较y₁与y₁的大小；
（3）当线段OA被l只分为两部分，且这两部分的比是1：4时，求h的值．