在一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
(1)第一小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图1);再沿GC折叠,使点B落在EF上的点B'处(如图2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.
(2)第二小组的同学,在一个矩形纸片上按照图3的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图4.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.
(3)探究活动结束后,老师给大家留下了一道探究题:
如图5,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,
请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为 ,
,
直线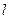 :
: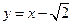 与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与
与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与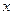
轴相切于点M.
求点A的坐标及∠CAO的度数
⊙B以每秒1个单位长度的速度沿
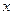 轴向右平移,同时,直线
轴向右平移,同时,直线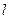 绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线
绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线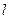 也恰好与⊙B第一次相切,问:直线
也恰好与⊙B第一次相切,问:直线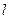 绕点A
绕点A
每秒旋转多少度?如图2,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,
当点E在劣弧AO上运动时(不与A、O两点重合), 的值是否发生变化?如
的值是否发生变化?如
果不变,求其值;如果变化,说明理由.
如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形ABCD的边长为2,E是AD的中点,按CE将菱形ABCD剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.
(1)在下面的菱形斜网格中画出示意图;
 |
|
|
(2)判断所拼成的三种图形的面积( )、周长(
)、周长( )的大小关系(用“=”、“>”或“<”连接):
)的大小关系(用“=”、“>”或“<”连接):
如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).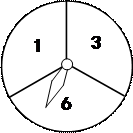
(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.
如图所示, 在正方形网格中,若点
在正方形网格中,若点 的坐标为
的坐标为 ,按要求回答下列问题:
,按要求回答下列问题:
在图中建立正确的平面直角坐标系;
根据所建立的坐标系,写出点
 和点
和点 的坐标;
的坐标;作出
 关于
关于 轴的对称图形
轴的对称图形 .(不用写作法)
.(不用写作法)
【原创】(本小题满分6分)
(1)画图,已知线段a和锐角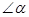 ,求作Rt△ABC,使它的一边为a,一锐角为
,求作Rt△ABC,使它的一边为a,一锐角为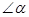 (不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可)。
(不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可)。
(2)回答问题:
满足上述条件的大小不同的共有________种。 ②若
②若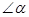 =
=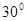 ,求最大的Rt△ABC的面积。
,求最大的Rt△ABC的面积。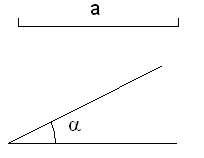
阅读下列材料:
在学习小组,小明接到这样一个任务:把一个正方形分割成9个、10个和11个小正方形。为完成任务,小明先学习了两种简单的“基本分割法”。
基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.
基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.
学习了上述两种“基本分割法”后,小明很从容地就完成了分割的任务:
(1)把一个正方形分割成9个小正方形.
方法一:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成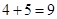 (个)小正方形.
(个)小正方形.
方法二:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成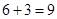 (个)小正方形.
(个)小正方形.
(2)把一个正方形分割成10个小正方形.
如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加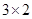 个小正方形,从而分割成
个小正方形,从而分割成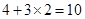 (个)小正方形.
(个)小正方形.
请你参照上述分割方法解决下列问题(只要求画图,不用说明分割方法):
(1)请你替小明同学把图⑥给出的正方形分割成11个小正方形;
(2)仿照基本分割法1:请把图a中的正三角形分割成4个小正三角形;
(3)仿照基本分割法2:请把图b 中的正三角形分割成6个小正三角形;
(4)分别把图c和图d中的正三角形分割成9个和10个小正三角形.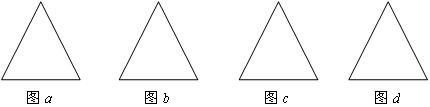
(本小题满分6分)
常用的确定物体位置的方法有两种. 
如图,在4×4个边长为1的正方形组成的方格中,标有A,B两点. 请你用两种不同方法表述点B相对点A的位置.
阅读下列材料
将图1的平行四边形用一定方法可分割成面积相等的八个四边形,如图2,再将图2中的八个四边形适当组合拼成两个面积相等且不全等的平行四边形.(要求:无缝隙且不重叠)
请你参考以上做法解决以下问题:
(1)将图4的平行四边形分割成面积相等的八个三角形;
(2)将图5的平行四边形用不同于(1)的分割方案,分割成面积相等的八个三角形,再将这八个三角形适当组合拼成两个面积相等且不全等的平行四边形,类比图2,图3,用数字 1至8标明.
1至8标明.
(3)设每个小格点正方形的边长为1,请你直接写出在(2)中拼成的两个不全等的平行四
边形的周长。
现有一张长和宽之比为2:1的长方形纸片.将它折两次(第一次折后也可以打开铺平再折第二次).使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作),如图甲(虚线表示折痕).
除图甲外,请你再给出三个不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图乙和图甲是相同的操作).
图① 图② 图③
(6分) 如图①、图②、图③……是用围棋子摆成的一列具有一定规律的“山”字.
(5) 按图示的规律填空.
| 图形标号 |
① |
② |
③ |
④ |
…… |
| 围棋子的数目(颗) |
7 |
|
|
|
|
(6) 第n个图形所对应的围棋子的数目为___________颗.
若某个图形中有围棋子142颗,它是第__________个图形.
如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)4节链条长 cm;
(2)n节链条长 cm;
(3)如果一辆22型自行车的链条由50节这样的链条组成,那么这辆自行车上的链条总长度是多少?
(本题8分)老师说:“今天我来表演一个数学魔术。”说完便在黑板上画出下面两个图:
⑴请你借助数学知识对这两个图通过计算验证说明拼接是否可行,若不行请说明理由;
⑵画出正确的拼接图(单位
 ),并作简单说明.
),并作简单说明.
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?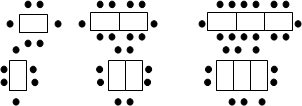
试题篮
()