如图,为测量一幢大楼的高度,在地面上距离楼底O点20 m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为(结果保留3个有效数字).
| A.42.8 m | B.42.80 m | C.42.9 m | D.42.90 m |
如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为
| A.4 cm | B.5 cm | C.6 cm | D.10 cm |
如图,在△ABC中,AB = AC,AB = 8,BC = 12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )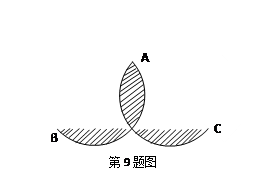
A.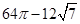 B.
B.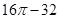 C.
C.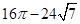 D.
D.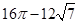
如图,
在△ABC中,CD是∠ACB的平分线,∠A = 80°,∠ACB=60°,那么∠BDC=( )
| A.80° | B.90 | C.100° | D.110° |
如图2, 、
、 、
、 分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是
分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是
A B C D
如图,坐标平面内一点A(2,-1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( )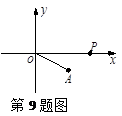
| A.2 | B.3 | C.4 | D.5 |
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数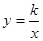 的图象上.那么k的值是
的图象上.那么k的值是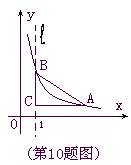
A .3 B.6 C.12 D.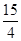
△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若 的长为12cm,那么
的长为12cm,那么 的长是
的长是
| A.10cm | B.9cm | C.8cm | D.6cm |
一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么
∠CME+∠BNF是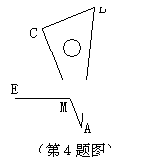
| A.150° | B.180° | C.135° | D.不能确定 |
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且ÐADE=60°,BD=3,CE=2,则△ABC的边长为

| A.9 | B.12 | C.15 | D.18 |
如图,在方格纸上建立的平面直角坐标系中,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△FEC,则点A的对应点F的坐标是
| A.(-1,1) | B.(-1,2) | C.(1,2) | D.(2,1) |
如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m
(即小颖的眼睛距地面的距离),那么这棵树高是( )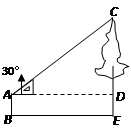
A.( )m )m |
B.(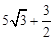 )m )m |
C.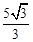 m m |
D.4m |
已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数所有可能的情况是
| A.0,1,2,3 | B.0,1,2,4 | C.0,1,2,3,4 | D.0,1,2,4,5 |
若一个三角形三个内角度数的比为2︰3︰4,那么这个三角形是
| A.直角三角形 | B.锐角三角形 | C.钝角三角形 | D.等边三角形 |
试题篮
()