如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ). 
(A)35 (B)40 (C)81 (D)84
在等边三角形ABC所在的平面内存在点P,使⊿PAB、⊿PBC、⊿PAC都是等腰三角形.请指出具有这种性质的点P的个数( )
(A)1 (B)7 (C)10 (D)15
如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
如图,在直角坐标系中,已知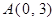 、
、 、
、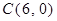 、
、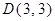 ,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.
,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.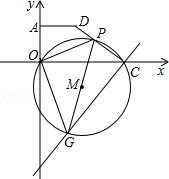
(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
如图,点A是5×5网格图形中的一个格点,图中每个小正方形的边长为1,请在网格中按下列要求操作: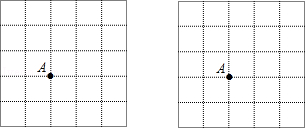
(1)以点A为其中的一个顶点,在图(1)中画一个面积等于3的格点直角三角形;
(2)以点A为其中的一个顶点,在图(2)中画一个面积等于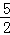 的格点等腰直角三角形.
的格点等腰直角三角形.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,即OD⊥AB于点D,OE⊥AC于点E,OD=OE,且OB=OC。
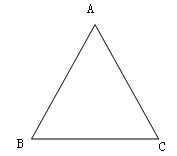
(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示(只需画图即可)。
在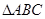 中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.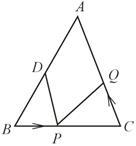
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若 ,求出发几秒后,
,求出发几秒后, 为直角三角形?
为直角三角形?
(3)若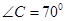 ,当
,当 的度数为多少时,
的度数为多少时, 为等腰三角形?(请直接写出答案,不必写出过程).
为等腰三角形?(请直接写出答案,不必写出过程).
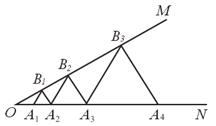
如图,已知∠MON=30°,点A1、A2、A3 …在射线ON上,点B1、B2、B3 …在射线OM上,△A1B1A2、△A2B2 A3、△A3B3 A4…均为等边三角形,若OA1=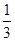 ,则△A2015 B2015 A2016的边长为 .
,则△A2015 B2015 A2016的边长为 .
在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD。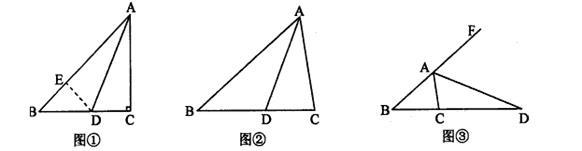
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明。
如图是一个三级台阶,它的每一级的长、宽和高分别为5 dm、3 dm和1 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是 dm.

如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了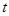 秒。
秒。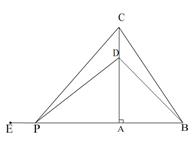
(1)求AD的长;
(2)直接写出用含有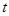 的代数式表示PE=_________;
的代数式表示PE=_________;
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出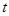 值;若不存在,请说明理由.
值;若不存在,请说明理由.
如图,在直角坐标系 中,直线AB交
中,直线AB交 轴于A(2,0),交
轴于A(2,0),交 轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
(1)求△ABC的面积.
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标.
(3)如图,D是第三象限内一动点,直线BE⊥CD于E, OF⊥OD交BE延长线于F.当D点运动时, 的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④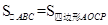 .其中所有正确结论的序号为( )
.其中所有正确结论的序号为( )
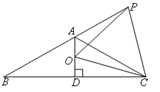
| A.①②③ | B.①②④ | C.①③④ | D.①②③④ |
试题篮
()