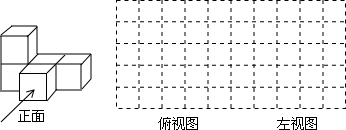
(1)由大小相同的小立方块搭成的几何体如下图,请在下图的方格中画出该几何体的俯视图和左视图.
(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
如图是由六个小正方体堆积而成,分别画出从正面看、从上面看、从左面看后的图形.
苏科版七年级(上册第119页)这样写道:
棱柱的侧棱长相等,棱柱的上下底面是相同的多边形,直棱柱的侧面都是长方形.底面是正三角形的直棱柱叫正三棱柱.
现给出两块面积相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明.
如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.
如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.

现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
马小虎准备制作一个封闭的正方体纸盒子,他先用5个大小一样的正方形纸板制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,需要在给出的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体纸盒子。请你帮助马小虎画上所拼接的正方形。(要求:①画出两种不同的拼接法;②添加的正方形用阴影表示)
知识背景:恩施来凤有一处野生古杨梅群落,其野生杨梅是一种具特殊价值的绿色食品.在当地市场出售时,基地要求“杨梅”用双层上盖的长方体纸箱封装(上盖纸板面积刚好等于底面面积的2倍,如图)
实际运用:如果要求纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米.
①按方案1(如图)做一个纸箱,需要矩形硬纸板 的面积是多少平方米?
的面积是多少平方米?
②小明认为,如果从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.
用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形和侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角不再利用).A方法:剪6个侧面;B方法:剪4个侧面和5个底面.现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面各数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
(1)由大小相同的边长为1小立方块搭成的几何体如图,请画出这个几何体的三视图并用阴影表示出来;.
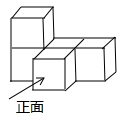
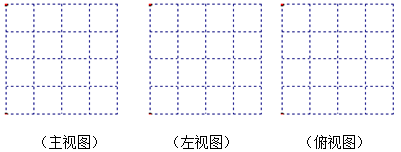
(2)根据三视图:这个组合几何体的表面积为 个平方单位.(包括底面积)
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
下图是一个几何体的平面展开图,每个面内都注上了字母,请回答下列问题:
(1)如果面B在几何体的前面,那么哪一面在后面?
(2)如果面E在几何体的底部,那么哪一面在上面?
(3)如果面D在前面,面F在左面,那么哪一面在上面?哪一面在右面?哪一面在底部?
某农户计划利用现有的一面墙(现在的墙足够长),建造如图所示的长方体水池,培育不同品种的鱼苗,他已备足可以修高为1.5 m,长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm(不考虑墙的厚度).
(1)若想水池的总容积为36 m3,x应等于多少?
(2)若想使水池的总容积V最大,x应为多少?最大容积是多少?
试题篮
()