初中数学立体图形解答题

如图，把长为40cm，宽30cm的长方形硬纸板，剪掉2个小正方形和2个小长方形（阴影部分即剪掉的部分），将剩余的部分拆成一个有盖的长方体盒子，设剪掉的小正方形边长为xcm（纸板的厚度忽略不计）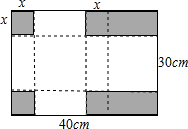

（1）长方体盒子的长、宽、高分别为多少？（单位：cm）
（2）若折成的一个长方体盒于表面积是950cm²，求此时长方体盒子的体积．

(1)左下图是有几个大小完全一样的小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,请你画出该几何体的主视图和左视图.

                       

	主视图		左视图

 

 
(2)如图，点P是 的边OB上的一点
①过点P画OB的垂线，交OA于点C
②过点P画OA的垂线，垂足为H
③线段PH的长度是点P到　　   的距离，
        是点C到直线OB的距离。
因为        所以线段PC、PH、OC这三条线段大小关系是　　　　（用“<”号连接）
（23--25题每题8分，共24分）

将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现在有一个长为4cm、宽为3cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱体，它们的体积分别是多大？

棱长为1cm的小正方形组成如图所示的零件模型，要将模型表面油漆成紫色（黏合的部分及地面接触部分不油漆）。

求：模型的涂漆面积；  
若模型表面涂漆加工费为5元每平方厘米，
那么这个模型的总加工费是多少元？

(8分)如图,长方体的长为15，宽为10，高为20，点B离点C的距离是5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？

（本题6分）已知一个几何体的三视图和有关尺寸如图所示，其中主视图为直角三角形，
∠ACB=Rt∠，说出这个几何体的名称，并求出这个几何体的表面积。

 

如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数．请你画出它的主视图与左视图．

已知直四棱柱的底面是边长为a的正方形， 高为, 体积为V, 表面积等于S. 当a =" 2," h =时，分别求V和S．

长12米，宽5米，高3米的教室，抹上石灰，扣除门窗黑板面积9．8平方米， 抹石灰的面积有多少平方米?

回答下列问题：
⑴如图所示的甲、乙两个平面图形能折什么几何体？

（2）由多个平面围成的几何体叫做多面体.若一个多面体的面数为，顶点个数为，棱数为，分别计算第（1）题中两个多面体的的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数.

(10分)某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒．

（1）现有正方形纸板162张，长方形纸板340张．若要做两种纸盒共l00个，设做竖式纸盒x个．
①      根据题意，完成以下表格：

纸盒 纸板	竖式纸盒(个)	横式纸盒(个)
x	100－x
正方形纸板(张)	▲	2(100－x)
长方形纸板(张)	4x	▲

 
②按两种纸盒的生产个数来分，有哪几种生产方案?
(2)若有正方形纸162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜306．求 a的值．

学校在艺术周上，要求学生制作一个精美的轴对称图形，请你用所给出的几何图形：○○△△    （两个圆，两个等边三角形，两条线段）为构件，构思一个独特，有意义的轴对称图形，并写上一句简要的解说词。

七巧板是我们祖先的一项卓越创造，用它可以拼出多种图形，请你用七巧板中标号为①②③的三块板（如图1）经过平移、旋转拼成图形．
（1）拼成矩形，在图2中画出示意图．
（2）拼成等腰直角三角形，在图3中画出示意图．
注意：相邻两块板之间无空隙，无重叠；示意图的顶点画在小方格顶点上．

如图，长方体的底面边长分别为1cm和3cm，高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达B(B为棱的中点)，那么所用细线最短需要多长？如果从点A开始经过4个侧面缠绕n圈到达点B，那么所用细线最短需要多长？

请画出下图的三视图