初中数学解答题

已知抛物线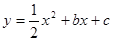的图像经过点O（0，0）A（6，0）。
（1）b =     ，c =     ；
（2）点B是x正半轴上的一动点，以OB为边在第一象限作一个正方形OBCD，使其一个顶点在抛物线上（不包括B点  ），画出示意图，求点B的坐标；
（3）在（2）的条件下，点E是线段BC上的一个动点，连结DE交线段AC与点F，则线段DF是否存在最小值，如果存在，请求出结果，如果不存在，请说明理由；

已知一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球．
（1）求从中随机抽取出一个黑球的概率是多少？
（2）若往口袋中再放入个白球和个黑球，从口袋中随机取出一个白球的概率是，求与之间的函数关系式．

如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AE=弧 AB，BE分别交AD、AC于点F、G．

（1）判断△FAG的形状，并说明理由；
（2）若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由．

已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．解答下列问题：

（1）当t为何值时，四边形APFD是平行四边形？
（2）设四边形APFE的面积为y（cm²），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S_{四边形APFE}：S_菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．

（1）（用公式法）         
（2） 3x²-4x-6=0（配方法解）                               
（3）（用合适的方法）  
（4）（用合适的方法）

因式分解：

解方程

因式分解：

已知y＋2与x成正比例，且x＝3时y＝1．
（1）写出y与x之间的函数关系式；
（2）求当x＝－1时，y的值；
（3）求当y＝0时，x的值．

如图，在平面直角坐标系中，AD＝8，OD＝OB，□ABCD的面积为24，求平行四边形的4个顶点的坐标．

有理数<0 、>0 、>0，且．
（1）在数轴上将a、b、c三个数填在相应的括号中．

（2）化简：．

解方程：
（1）；
（2）

（1）化简：2a-[a-2（a-b）]-b
（2）先化简，再求值：已知多项式A＝3²—6ab＋b²，B＝—2²＋3ab—5b²，当=1，b=—1时，求A+2B的值．

爱动脑筋的小明在学习了全等三角形和等腰三角形有关知识后作了如下探索：
（1）已知，如图，△ABC中，∠BAC是锐角，AB＝AC，高AD、BG 所在的直线相交于点H， 且AG＝BG，则AH和BC的关系是：_____________________；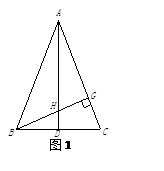

（2）若把（1）中的“∠BAC是锐角”改为“∠BAC是钝角”（如图2），其他条件都不变， AH和BC的关系是否仍然成立， 若成立，请在图2中用三角板和量角器画出完整的图形并证明；若不成立，请说明理由．

如图，C为线段AB的中点，CD∥BE，CD＝BE．求证：AD∥CE．