初中数学解答题

口袋中有4个分别写着字母A、B、C、D的小球，这些小球除字母外都相同，现在随机抽取一个小球后放回，再随机抽取一个小球．
（1）用画树状的方法表示所有可能的结果；
（2）求两次取得相同字母的概率．

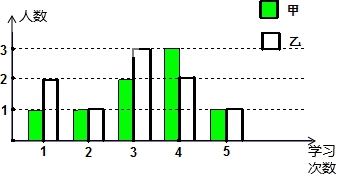
为了了解温州市中学生开展研究性学习的情况，抽查了某中学九年级甲、乙两班的部分学生，了解他们在一个月内参加研究性学习的情况，结果统计如下：
（1）在这次抽查中甲班被抽查了       人，乙班被抽查了         人；
（2）被抽查的学生中，甲班学生参加研究性学习的平均次数为       次，中位数是      次，乙班学生参加研究性学习的平均次数为         次，中位数是            次；
（3）根据以上信息，用你学过的统计知识，推测甲、乙两班在开展研究性学习方面哪个班级更好一些？

已知二次函数y=x²+2x-3．
（1）求此二次函数的图象与x轴的交点坐标；
（2）此二次函数的图象经怎样平移，使顶点变为A（3，0），请你描述平移的过程．

七年级我们学过三角形的相关知识，在动手实践的过程中，发现了一个基本事实：
三角形的三条高（或三条高所在直线）相交于一点．
其实，有很多八年级、九年级的问题均可用此结论解决．
【运用】如图，已知：△ABC的高AD与高BE相交于点F，且∠ABC=45°，过点F作FG∥BC交AB于点G，求证：FG+CD=BD．

小方同学在解答此题时，利用了上述结论，她的方法如下：
连接CF并延长，交AB于点M，
∵△ABC的高AD与高BE相交于点F，
∴CM为△ABC的高．
（请你在下面的空白处完成小方的证明过程．）
【操作】如图AB是圆的直径，点C在圆内，请仅用无刻度的直尺画出△ABC中AB边上的高．

解方程：4t²-（t+1）²=0．

解方程
（1）x²+2x-2="0"
（2）（x+2）²-10（x+2）+25=0．

如图，抛物线y=﹣x²+bx+c与x轴交于A（1，0），B（﹣4，0）两点，

（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得?QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
（3）设此抛物线与直线y=﹣x在第二象限交于点D，平行于y轴的直线x=m（-1-＜m＜0）与抛物线交于点M，与直线y=﹣x交于点N，连接BM、CM、NC、NB，是否存在m的值，使四边形BNCM的面积S最大？若存在，请求出m的值，若不存在，请说明理由．

如图所示，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H．

（1）如果⊙O的半径为4，CD=，求∠BAC的度数；
（2）若点E为的中点，连接OE，CE．求证：CE平分∠OCD；
（3）在（1）的条件下，圆周上到直线AC距离为3的点有多少个？并说明理由．

某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于65元，市场调查发现，若每箱以50元的价格出售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．
（1）求平均每天销售量y（箱）与涨价x（元/箱）之间的函数关系式；
（2）求当每箱苹果的销售价为多少元，批发商平均每天的销售利润W（元）可以获得最大？

如图，AB为的直径，AB=AC，BC交于点D，AC交于点E．

（1）求证：BD=CD；
（2）若AB=8，∠BAC=45°，求阴影部分的面积．

解方程：．

解方程：x²+4x+2=0．

李军同学早晨起来跑步，他从自家向东跑了2千米到达谢彬家，继续向东跑了1．5千米到达红红家，然后向西跑了4．5千米到达了学校，最后回到家．请按要求完成下列各题．
（1）以李军家为原点，以向东的方向为正方向，用1个单位长度表示1千米，请你画出数轴，并在数轴上表示出李军、谢彬、红红家及学校的位置及各位置表示的有理数；
（2）谢彬家距学校多远？
（3）李军一共跑了多少千米？

如图，在平面直角坐标系内，梯形OABC的顶点坐标分别是：A（3，4），B（8，4），C（11，0），点P（t，0）是线段OC上一点，设四边形ABCP的面积为S．

（1）过点B作BE⊥x轴于点E，则BE=         ，用含t的代数式表示PC=           ．
（2）求S与t的函数关系．
（3）当S＝20时，直接写出线段AB与CP的长．

化简
（1）－5+4m－2mn+6+3mn    
（2）2（2a－3b）－3（2b－3a）