(本小题满分12分)如图,直线 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0).
轴于另一点C(3,0).
⑴ 求抛物线的解析式;
⑵ 在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
(本题满分10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)写出 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段 上是否存在点
上是否存在点 ,使
,使
 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分8分)
如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A与原起点B的距离 (精确到0.1米).
(精确到0.1米).
(本小题满分8分)
已知如图,点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF;(2)BE=CF.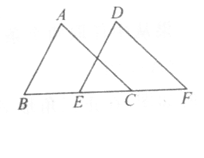
如图,直线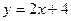 与
与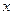 轴、
轴、 轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.
轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.
⑴在图中画出△OCD;
⑵求经过A、B、D三点的抛物线的解析式;
⑶点P在抛物线对称轴上运动
①当直线CP把△OCD分成面积相等的两部分时,试求出点P的坐标;
②是否存在点P,使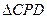 为直角三角形,若存在,请求出点
为直角三角形,若存在,请求出点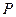 的坐标;如果不存在,请
的坐标;如果不存在,请
说明理由.
(9分)如图所示,在边长为1的正方形ABCD中,一直角三角尺PQR的直角顶点P在对角线AC上移动,直角边PQ经过点D,另一直角边与射线BC交于点E.
⑴试判断PE与PD的大小关系,并证明你的结论;
⑵连 接PB,试证明:△PBE为等腰三角形;
接PB,试证明:△PBE为等腰三角形;
⑶设AP=x,△PBE的面积为y,
①求出y关于x 函数关系式;
②当点P落在AC的何处时,△PBE的面积最大,此时最大值是多少?
操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在 斜边AB的中点P处,
斜边AB的中点P处, 将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点,如图3-1-13①②③是旋转三角板得到的图形中的3种情况,
将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点,如图3-1-13①②③是旋转三角板得到的图形中的3种情况,
由①②③研究:(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图①加以证明。
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长;若不能,请说明理由)。
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图④加以证明。



如图,已知抛物线y=x2+bx+c经过A(1,0),B (0,2)两点,顶点为D。
(0,2)两点,顶点为D。
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与y轴的交点为B,顶点为D,若点N 在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标。
在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标。
如图所示,电工李师傅借助梯子安装天花板上距地面2.90m的顶灯,已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m,矩形面与地面所成的角α为78°,李师傅的身高为1.78m,当他攀升到头顶距天花板0.05~0.20m时,安装起来比较方便。
(1)为了安全在梯子的第二段间接一根绳子,绳子最短应是多少?(两边打结处共用绳0.6m)
(2)他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他 安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.
①试探究AE与⊙O的位置关系,并说明理由;
②已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,设计出计算⊙O的半径r的一种方案;
1) 你选用的已知数是_________;
2) 写出求解过程(结果用字母表示).
如图:抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点Q(x,0)是x轴上的一动点,过Q点作x轴的垂线,交抛物线于P点、交直线BA于D点,连结OD,PB,当点Q(x,0)在x轴上运动时,求PD与x之间的函数关系式;四边形OBPD能否成为平行四边形,若能求出Q点坐标,若不能,请说明理由。
(3) 是否存在一点Q,使以PD为直径的圆与y轴相切,若存在,求出Q点的坐标;若不存 在,请说明理由.
在,请说明理由.

为了加强市民的节水意识,合理利用水资源,某市采用价格调控手段达节水的
目的。该市自来水收费价格价目表:
(1)居民甲2月份用水12.5 ,则应收水费元;
,则应收水费元;
(2)居民乙3、4月份用水15 ,(4月份用水量超过3月份),共交水费44元,求这户居民3、4月份的用水量。
,(4月份用水量超过3月份),共交水费44元,求这户居民3、4月份的用水量。
如图1,在四边形ABCD的AB边上任取一点E(点E不与点A、点B
重合),分别连接ED、EC,可以把四边形ABCD分成3个三角形.如果其中有2个三角形
相似,我们就把点E叫做四边形ABCD的AB边上的相似点;如果这3个三角形都相似,
我们就把点E叫做四边形ABCD的AB边上的强相似点.
(1)若图1中,∠A=∠B=∠DEC=50°,说明点E是四边形ABCD的AB边上的相似点;
(2)①如图2,画出矩形ABCD的AB边上的一个强相似点.(要求:画图工具不限,不写画法,保留画图痕迹或有必要的说明.)
②对于任意的一个矩形,是否一定存 在强相似点?如果一定存在,请说明理由;如果不一定存在,请举出反例.
在强相似点?如果一定存在,请说明理由;如果不一定存在,请举出反例.
(3)在梯形ABCD中,AD∥BC,AD<BC,∠B=90°,点E是梯形ABCD的AB边上的一个强相似点,判断AE与BE的数量关系并说明理由.
(1)在遇到问题:“钟 面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2
面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2 ∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面 内
内
的两条线段,在7∶30~8∶00之间,时针与分针互相垂直的时刻是多少?
试题篮
()