初中数学解答题

(Ⅰ)某服装厂承揽一项生产夏凉小衫1600件的任务，计划用 $t$天完成．
（1）写出每天生产夏凉小衫 $w$（件）与生产时间 $t$（天）（ $t>4$）之间的函数关系式;
（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？
(Ⅱ)如图，已知矩形 $ABCD$中， $E$是 $AD$上的一点， $F$是 $AB$上的一点， $EF\perp EC$，且 $EF=EC$， $DE=4cm$，矩形 $ABCD$的周长为32cm，求 $AE$的长．

(1)（本小题满分4分）计算：．
(2)（本小题满分6分）
进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这
是记者与驻军工程指挥官的一段对话:

通过这段对话,请你求出该地驻军原来每天加固的米数.

如图，已知二次函数y=ax²+2x+c（a＞0）图象的顶点M在反比例函数上，且与x轴交于AB两点．
（1）若二次函数的对称轴为，试求a，c的值；
（2）在（1）的条件下求AB的长；
（3）若二次函数的对称轴与x轴的交点为N，当NO+MN取最小值时，试求二次函数的解析式．

如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，过点D作DE⊥AC，垂足为E．
（1）求证：DE是⊙O的切线；
（2）如果BC=8，AB=5，求CE的长．

一场特大暴雨造成遂渝高速公路某一路段被严重破坏。为抢修一段120米长的高速公路，施工队每天比原计划多修5米，结果提前4天完成抢修任务。问原计划每天抢修多少米？

在同一平面内有n条直线，任何两条不平行，任何三条不共点。
当n=1时，如图⑴，一条直线将一个平面分成两个部分；
当n=2时，如图⑵，两条直线将一个平面分成四个部分；

则：当n=3时，三条直线将一个平面分成部分；
当n=4时，四条直线将一个平面分成部分；
若n条直线将一个平面分成个部分，
n+1条直线将一个平面分成个部分。
试探索、、n之间的关系。

平面直角坐标系中，直线AB交x轴于点A，交y轴于点B且与反比例函数图像分别交于C、D两点，过点C作CMx轴于M，AO=6，BO=3，CM=5。求直线AB的解析式和反比例函数解析式。

已知AB是⊙的直径，弦AC平分，ADCD于D，BECD于E。
求证：⑴CD是⊙的切线；
⑵

2014年遂宁市将承办四川省运动会。明星队和沱牌队在集训期内进行了五场比赛，将比赛成绩进行统计后，绘制成如图①、图②的统计图。
⑴在图②中画出表示沱牌队在集训期内这五场比赛的成绩变化情况的折线统计图；
⑵请你分别计算明星队和沱牌队这五场比赛的平均分；
⑶就五场比赛，分别计算两队成绩的极差；
⑷如果从明星与沱牌中选派一支参加省运会，根据上述统计情况，从平均分、折线走势、获胜场数和极差四个方面进行简要分析，请你决策选派哪支球队参加更能取得好的成绩？

在“我爱家乡”的主题活动中，某数学兴趣小组决定测量灵泉寺观音塔DC的高度（如图）。在广场A处用测角仪测得塔顶D的仰角是45°，沿AC方向前进15米在B处测得塔顶D的仰角是60°，测角仪高1.5米。求塔高DC（保留3个有效数字）（）

已知：平行四边形ABCD中，过对角线AC中点O的直线EF交AD于F，BC于E。
求证：BE=DF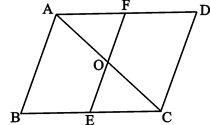

解方程：

如图，已知二次函数 $y=x^2+bx+c$的图象的对称轴为直线 $x=1$，且与 $x$轴有两个不同的交点，其中一个交点坐标为 $(-1,0)$．
（1）求二次函数的关系式；
（2）在抛物线上有一点 $A$，其横坐标为-2，直线 $l$过点 $A$并绕着点 $A$旋转，与抛物线的另一个交点是点 $B$，点 $B$的横坐标满足 $﹣2＜x_B＜\frac{3}{2}$，当 $△AOB$的面积最大时，求出此时直线 $l$的关系式；
（3）抛物线上是否存在点 $C$使 $△AOC$的面积与（2）中 $△AOB$的最大面积相等．若存在，求出点 $C$的横坐标；若不存在说明理由．

如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．
（1）求抛物线的函数表达式；
（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．
①求S关于m的函数表达式，并求出m为何值时，S取得最大值；
②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

如图1，△ABC中，∠C=90°，∠ABC=30°，AC=m，延长CB至点D，使BD=AB．
①求∠D的度数；
②求tan75°的值．
（2）如图2，点M的坐标为（2，0），直线MN与y轴的正半轴交于点N，∠OMN=75°．求直线MN的函数表达式．