初中数学解答题

某小学在6月1日组织师生共110人到趵突泉公园游览，趵突泉公园规定：成人票价每位40元，学生票价每位20元．该学校购票共花费2400元，在这次游览活动中，教师和学生各有多少人？

（1）如图1，△ABC中，∠A=60°，∠B：∠C=1：5，求∠B的度数．
（2）如图2，点M为正方形ABCD对角线BD上一点，分别连接AM、CM．求证：AM=CM．

（1）计算：（a+b）（a﹣b）+2b²．
（2）解方程：．

（11·天水）在梯形OABC中，CB∥OA，∠AOC＝60°，∠OAB＝90°，
OC＝2，BC＝4，以点O为原点，OA所在的直线为x轴，建立平面直角坐标系，另有一边
长为2的等边△DEF，DE在x轴上（如图（1）），如果让△DEF以每秒1个单位的速度向
左作匀速直线运动，开始时点D与点A重合，当点D到达坐标原点时运动停止．
（1）设△DEF运动时间为t，△DEF与梯形OABC重叠部分的面积为S，求S关于t的函
数关系式．
（2）探究：在△DEF运动过程中，如果射线DF交经过O、C、B三点的抛物线于点G，是
否存在这样的时刻t，使得△OAG的面积与梯形OABC的面积相等？若存在，求出t的值；
若不存在，请说明理由．
 

（11·天水）在△ABC中，AB＝AC，点O是△ABC的外心，连接AO
并延长交BC于D，交△ABC的外接圆于E，过点B作⊙O的切线交AO的延长线于Q，设

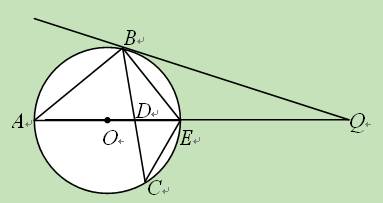
（11·天水）某电脑公司各种品牌、型号的电脑价格如下表，育才中学
要从甲、乙两种品牌电脑中各选择一种型号的电脑．
（1）写出所有选购方案（利用树状图或列表方法表示）．如果各种选购方案被选中的可能性
相同，那么A型号电脑被选中的概率是多少？
（2）该中学预计购买甲、乙两种品牌电脑共36台，其中甲品牌电脑只选了A型号，学校
规定购买费用不能高于10万元，又不低于9.2万元，问购买A型号电脑可以是多少台？

	甲	乙
型号	A	B	C	D	E
单价（元/台）	6000	4000	2500	5000	2000

（11·天水）某校开展的一次动漫设计大赛，杨帆同学运用了数学知识
进行了富有创意的图案设计，如图（1），他在边长为1的正方形ABCD内作等边△BCE，
并与正方形的对角线交于点F、G，制作如图（2）的图标，请我计算一下图案中阴影图形的
面积．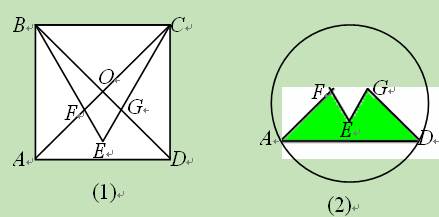

（11·天水）如图，在平面直角坐标系中，O为坐标原点，每个小方格的
边长为1个单位长度．正方形ABCD顶点都在格点上，其中，点A的坐标为 (1，1)．
（1）若将正方形ABCD绕点A顺时针方向旋转90°，点B到达点B₁，点C到达点C₁，点
D到达点D₁，求点B₁、C₁、D₁的坐标．
（2）若线段AC₁的长度与点D₁的横坐标的差恰好是一元二次方程x²＋ax＋1＝0的一个根，
求a的值．
  

（11·天水）本题共13分（其中第Ⅰ小题6分，第Ⅱ小题7分）
Ⅰ．爱养花的李先生为选择一个合适的时间去参观2011年西安世界园艺博览会，他查阅了
5月10日至16日是（星期一至星期日）每天的参观人数，得到图（1）、图（2）所示的统
计图．其中图（1）是每天参观人数的统计图，图（2）是5月15日（星期六）这一天上午、
中午、下午和晚上四个时段参观人数的扇形统计图，请你根据统计图解答下面的问题：
（1）5月10日至16日这一周中，参观人数最多的是日是_  ▲  ，有_  ▲  万人，
参观人数最少的是日是_  ▲  ，有_  ▲  万人，中位数是_  ▲  ．
（2）5月15日是（星期六）这一天，上午的参观人数比下午的参观人数多多少人？（精确
到1万人）
（3）如果李先生想尽可能选择参观人数较少的时间参观世园会，你认为选择什么时间较合
适？

Ⅱ．如图在等腰Rt△OBA和Rt△BCD中，∠OBA＝∠BCD＝90°，点A和点C都在双曲线

（11·天水）已知，如图E、F是四边形ABCD的对角线AC上的两点，AF＝CE，
DF＝BE，DF∥BE，四边形ABCD是平行四边形吗？请说明理由．

Ⅱ．已知l₁：直线y＝－x＋3和l₂：直线y＝2x，l₁与x轴交点为A．求：
（1）l₁与l₂的交点坐标．
（2）经过点A且平行于l₂的直线的解析式

(8分)“十年树木，百年树人”，教师的素养关系到国家的未来.我市某区招聘音乐
教师采用笔试、专业技能测试、说课三种形式进行选拔，这三项的成绩满分均为100分，并
按2:3:5的比例折合纳入总分，最后，按照成绩的排序从高到低依次录取.该区要招聘2名音
乐教师，通过笔试、专业技能测试筛选出前6名选手进入说课环节，这6名选手的各项成绩
见下表：

序号	1	2	3	4	5	6
笔试成绩	66	90	86	64	65	84
专业技能测试成绩	95	92	93	80	88	92
说课成绩	85	78	86	88	94	85

（1）笔试成绩的极差是多少？
（2）写出说课成绩的中位数、众数；
（3）已知序号为1,2,3,4号选手的成绩分别为84.2分，84.6分，88.1分，80.8分，请你判断这六位选手中序号是多少的选手将被录用？为什么？

(8分)如图，直线AB，CD分别与直线AC相交于点A，C，与
直线BD相交于点B，D．若∠1=∠2，∠3=75°，求∠4的度数．

（11·贺州）．
如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（A在B的左侧），与y轴交于
（1）求抛物线的函数表达式；
（2）设抛物线的对称轴与轴交于点D，试在对称轴上找出点P，使△CDP为等腰三角形，
请直接写出满足条件的所有点P的坐标．
（3）若点E是线段AB上的一个动点（与A、B不重合），分别连接AC、BC，过点E作EF
∥AC交线段BC于点F，连接CE，记△CEF的面积为S，S是否存在最大值？若存在，求
出S的最大值及此时E点的坐标；若不存在，请说明理由．

（11·贺州）
如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D．
锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线
交于点E．
（1）求证：AC平分∠DAB；
（2）过点O作线段AC的垂线OE，垂足为E（要求：尺规作图，保留作图痕迹，不写作
法）；