初中数学解答题

（11·贺州）
某校教学楼后面紧邻着一个山坡，坡上面是一块平地，如图所示，BC∥AD，BE⊥AD，斜坡AB长为26米，坡角∠BAD＝68°．为了减缓坡面防止山体滑坡，保障安全，学校决定对该斜坡进行改造，经地质人员勘测，当坡角不超过50°时，可确保山体不滑坡．
（1）求改造前坡顶到地面的距离BE的长（精确到0.1米）；
（2）如果改造时保持坡脚A不动，坡顶B沿BC向左移11米到F点处，问这样改造能确
保安全吗？
（参考数据：sin 68°≈0.93，cos 68°≈0.37，tan 68°≈2.48，sin 58°12’≈0.85，tan 49°30’
≈1.17）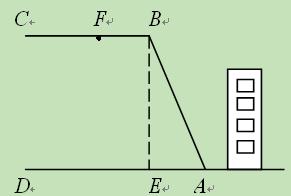

（11·贺州）
某生姜种植基地计划种植A、B两种生姜30亩．已知A、B两种生姜的年产量分别为2 000千克/亩、2 500千克/亩，收购单价分别是8元/千克、7元/千克．
（1）若该基地收获两种生姜的年总产量为68 000千克，求A、B两种生姜各种多少亩？
（2）若要求种植A种生姜的亩数不少于B种的一半，那么种植A、B两种生姜各多少亩时，
全部收购该基地生姜的年总收入最多？最多是多少元？

（11·贺州）
某校为了解九年级800名学生的体育综合素质，随机抽查了50名学生进行体育综合测试，所得成绩整理分成五组，并制成如下频数分布表和扇形统计图，请根据所提供的信息解答下列问题：

（1）频数分布表中的m＝_  ▲  ，n＝_  ▲  ；
（2）样本中位数所在成绩的级别是_  ▲  ，扇形统计图中，E组所对应的扇形圆心角的度数是_  ▲  ；
（3）请你估计该校九年级的学生中，体育综合测试成绩不少于80分的大约有多少人？

（11·贺州）
如图，在平面直角坐标系中，点O为原点，反比例函数的图象经过点(1，4)，菱
形OABC的顶点A在函数的图象上，对角线OB在x轴上．
（1）求反比例函数的关系式；
（2）直接写出菱形OABC的面积．

（11·贺州）
如图，E、F是平行四边形ABCD对角线AC上的两点，BE∥DF．求证：BE＝DF．

（本题满分10分，每小题5分）
（1）（11·贺州）

（2）（11·贺州）先化简，再求值：(a＋1) (a－1)＋a (1－a)，其中a＝2012．

如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=6cm，AB=8cm，BC=14cm.动点P、Q都从点C出发，点P沿C→B方向做匀速运动，点Q沿C→D→A方向做匀速运动，当P、Q其中一点到达终点时，另一点也随之停止运动．
（1）求CD的长；
（2）若点P以1cm/s速度运动，点Q以cm/s的速度运动，连接BQ、PQ，设△BQP面积为S（cm²），点P、Q运动的时间为t（s），求S与t的函数关系式，并写出t的取值范围；
（3）若点P的速度仍是1cm/s，点Q的速度为acm/s，要使在运动过程中出现PQ∥DC，请你直接写出a的取值范围．

（11·佛山）阅读材料
我们经常通过认识一个事物的局部或其特殊类型，来逐步认识这个事物；
比如我们通过学习两类特殊的四边形，即平行四边形和梯形（继续学习它们的特殊类型如矩形、等腰梯形等）来逐步认识四边形；
我们对课本里特殊四边形的学习，一般先学习图形的定义，再探索发现其性质和判定方法，然后通过解决简单的问题巩固所学知识；
请解决以下问题：
如图，我们把满足AB＝CD、CB＝CD且AB≠BC的四边形ABCD叫做“筝形”；
（1）写出筝形的两个性质（定义除外）；
（2）写出筝形的两个判定方法（定义除外），并选出一个进行证明；

（11·佛山）商场对某种商品进行市场调查，1至6月份该种商品的销售情况如下：
①销售成本p（元/千克）与销售月份x的关系如图所示：

③销售量m（千克）与销售月份x满足m＝100x＋200；
试解决以下问题：
（1）      根据图形，求p与x之间的函数关系式；
（2）      求该种商品每月的销售利润y（元）与销售月份x的函数关系式，并求出哪个月的
销售利润最大？

（11·佛山）现在初中课本里所学习的概率计算问题只有以下类型：
第一类是可以列举有限个等可能发生的结果的概率计算问题（一步试验直接列举，两步以上的试验可以借助树状图或表格列举），比如掷一枚均匀硬币的试验；
第二类是用试验或者模拟试验的数据计算频率，并用频率估计概率的概率计算问题，比如掷图钉的试验；
解决概率计算问题，可以直接利用模型，也可以转化后再利用模型；
请解决以下问题
（1）如图，类似课本的一个寻宝游戏，若宝物随机藏在某一块砖下（图中每一块砖除颜色外完全相同），则宝物藏在阴影砖下的概率是多少？

（2）在中随机选取3个整数，若以这3个整数为边长构成三角形的情况如下表：

请你根据表中数据，估计构成钝角三角形的概率是多少？（精确到百分位）

（11·佛山）如图，一张纸上有线段AB；
（1）请用尺规作图，作出线段AB的垂直平分线（保留作图痕迹，不写作法和证明）；
（2）若不用尺规作图，你还有其它作法吗？请说明作法（不作图）；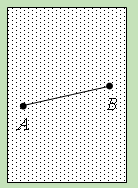

（11·佛山）如图，已知二次函数y＝ax²＋bx＋c的图像经过A（－1，－1）、B（0，2）、C（1，3）；
（1）求二次函数的解析式；
（2）画出二次函数的图像；

（11·佛山）如图，已知AB是⊙O的弦，半径OA＝20cm，∠AOB＝120°，求△AOB的面积；

（11·佛山）某市年的用电情况如下图1：

（1）求商业用电量与工业用电量之比是多少？
（2）请在图2上作出更加直观、清楚反映用电比例情况的条形图；

（11·佛山）如图，D是△ABC的边AB上一点，连结CD，若AD＝2，BD＝4，
∠ACD＝∠B，求AC的长；