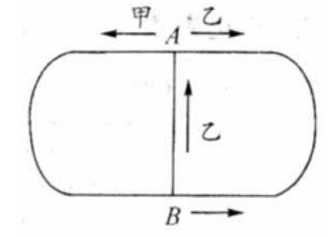
如图是一个长为 的环形跑道,其中 为跑道对称轴上的两点,且 之间有一条 的直线通道.甲乙两人同时从 点出发,甲按逆时针方向以速度 沿跑道跑步,当跑到 点时继续沿跑道前进,乙按顺时针方向以速度 沿跑道跑步,当跑到 点时沿直线通道跑回 点处,假设两人跑步的时间足够长.求:
(1)如果 ,那么甲跑了多少路程后,两人首次在 点处相遇;
(2)如果 ,那么乙跑了多少路程后,两人首次在 点处相遇.
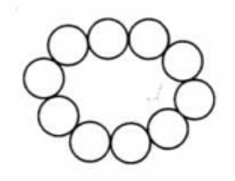
如图,将 这 个数字分别填入图中的 个圆圈内,使任意连续相邻的 个圆圈内的数字之和均不大于某一个整数 ,求 的最小值并完成相应的填图游戏.
用水平线和竖直线将平面分成若干个边长为 的小正方形格子,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为 ,它各边上格点的个数和为 .

(1)图①-④中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出 与 之间的关系式.
答 _____.

(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有 个格点.此时所画的各个多边形的面积 与它各边上格点的个数和 之间的关系是: _____.
(3)请你继续探索,当格点多边形内部有且只有 个格点时,猜想 与 有怎样的关系?
某城市有一段马路需要整修,这段马路的长不超过 ,今有甲、乙、丙三个施工队,分别施工人行道、非机动车道和机动车道.他们于某天零时同时开工,每天 连续施工.若干天后的零时,甲完成任务;几天后的 时,乙完成任务;自乙队完成的当天零时起,再过几天后的 时,丙完成任务.已知三个施工队每天完成的施工任务分别为 ,问这段路面有多长?
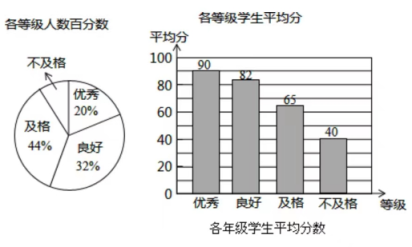
《中学生体质健康标准》规定学生体质健康等级标准为: 分及以上为优秀; 分~ 分为良好; 分~ 分为及格; 分以下为不及格.某校抽取八年级学生人数的 进行体质测试,测试结果如图.
(1)在抽取的学生中不及格人数所占的百分比是_____;
(2)小明按以下方法计算所抽取学生测试结果的平均分是 .根据所学的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式并计算出结果;
(3)若抽取的学生中不及格学生的总分恰好等于某一个良好等级学生的分数,请估算该校八年级学生中优秀等级的人数.
某校食堂在开晩餐前有 名学生在食堂排队等候就餐,开始卖晩餐后,仍有学生前来排队买晩餐.设学生前来排队买晩餐的人数按固定的速度增加,食堂每个窗口卖晩餐的速度也是固定的.若开放一个窗口,则需要 才使排队等候的学生全部买到晩餐;若同时开放两个窗口,则需 就可使排队等候的学生全部买到晩餐.
(1)写出开放一个窗口时,开始卖晩餐后窗口卖晩餐的速度 人 与每分钟新增加的学生人数 (人)之间的关系.
(2)食堂为了提高服务质量,减少学生排队的时间,计划在 内让排队等候的学生全部买到晩餐,以便于后到的学生能随到随买,至少要同时开放几个窗口?
某工程机械厂根据市场要求,计划生产 两种型号的大型挖掘机共 台,该厂所筹生产资金不少于 万元,但不超过 万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:

(1)该厂对这两种型号挖掘机有几种生产方案?
(2)该厂如何生产获得最大利润?
(3)根据市场调查,每台 型挖掘机的售价不会改变,每台 型挖掘机的售价将会提高 万元 ,该厂如何生产可以获得最大利润(注:利润 售价-成本)?
某果品商店进行组合销售,甲种搭配: 水果, 水果;乙种搭配: 水果, 水果, 水果;丙种搭配: 水果, 水果, 水果.已知 水果 元 水果 元 水果 元 .某天该商店销售这三种搭配水果共 元,其中 水果的销售额为 元,问 水果的销售额为多少元?
如图,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分成 个大小不同的正方形,请你计算:
(1)第 个正方形的边长为_____;第 个正方形的边长为_____;第 个正方形的边长为_____.(用含 的代数式表示)
(2)当 时,第 个正方形的面积为_____.
(3)当 均为正整数时,求这个完美长方形的最小周长.

如图①折线 是夹在两平行线 和 之间的一条折线.

(1)探求 与 之间的关系;
(2)若图①变化成图②,③,④,⑤,则各图中标注的角( )又有什么关系?请直接写出结论;
(3)如图⑥中,若 与 之间有什么关系?请直接写出结论.
一只青蛙在平面直角坐标系上从点 开始,可以按照如下两种方式跳跃:①能从任意一点 ,跳到点 或 ;②对于点 ,如果 ,则能从 跳到 ,如果 ,则能从 跳到 ,例如,按照上述跳跃方式,这只青蛙能够到达点 ,跳跃的一种路径为: ,请你思考:这只青蛙按照规定的两种方式跳跃,能达到下列各点吗?如果能,请分别给出从点 出发到指定点的路径;如果不能,请说明理由.
(1) ;(2) ;(3) ;(4) .
试题篮
()