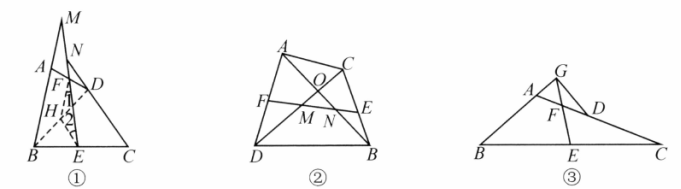
如图①,在四边形 中, 分别是 的中点,连接 并延长,分别与 的延长线交于点 ,则 .
(温馨提示:在图①中,连接 ,取 的中点 ,连接 ,根据三角形中位线定理,证明 ,从而 ,再利用平行线性质,可证 .)
(1)如图②,在四边形 中, 与 相交于点 分别是 的中点,连接 ,分别交 于点 ,判断 的形状,并给予证明;
(2)如图③,在 中, 点在 上, 分别是 的中点,连接 并延长,与 的延长线交于 ,若 ,连接 ,判断 的形状并证明.
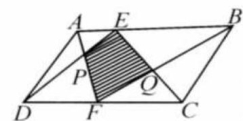
如图, 分别是 的边 上的点, 与 相交于点 与 相交于点 ,若 ,则阴影部分的面积_____为 .
平面上的一组 条平行线与另一组 条平行线相交,可构成平行四边形的个数为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知四边形 ,从下列条件中:① ⑤ ;⑥ .任取其中两个,可以得出“四边形 是平行四边形”这一结论的情况有( )
| A. | 种 |
B. | 种 |
C. | 种 |
D. | 种 |
如图,点 在平行四边形的对角线上,试判断 之间的大小关系( )

| A. |
|
B. |
|
C. |
|
D. | 无法确定 |
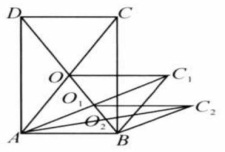
如图,长方形 的面积为 .对角线交于点 ,以 为邻边作平行四边形 ,对角线交于点 ;以 为邻边作平行四边形 ,以此类推,则 的面积为( )
| A. |
|
B. |
|
C. |
|
D. |
|
给出下列命题:①一组对边和一组对角分别相等的四边形是平行四边形;②两组对角的内角平分线分别平行的四边形是平行四边形;③一组对边中点间的距离等于另一组对边边长和的一半的四边形是平行四边形;④两条对角线都平分四边形面积的四边形是平行四边形.其中,真命题有( )
| A. | 个 |
B. | 个 |
C. | 个 |
D. | 个 |
试题篮
()