初中数学试题

如图，在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACFG，连接CE、BG和EG，EG与HA的延长线交于点M，有下列结论：①BG＝CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM＝∠ABC．其中正确结论的个数是（　　）

A．4
B．3
C．2
D．1

如图，边长为1的菱形ABCD中，∠DAB＝60°．连接对角线AC，以AC为边作第二个菱形ACEF，使∠FAC＝60°．连接AE，再以AE为边作第三个菱形AEGH，使∠HAE＝60°……按此规律所作的第n个菱形的边长是________．

把长与宽之比为的矩形纸片称为标准纸，请思考并解决下列问题：
(1)将一张标准纸ABCD(AB＜BC)对开，如图1所示，所得的矩形纸片ABEF是标准纸，请给予证明；

(2)在一次综合实践课上，小明尝试着将矩形纸片ABCD(AB＜BC)进行如下操作：
第一步：沿过A点的直线折叠，使B点落在AD边上点F处，折痕为AE(如图2甲)；
第二步：沿过D点的直线折叠，使C点落在AD边上点N处，折痕为DG(如图2乙)，此时E点恰好落在AE边上的点M处；
第三步：沿直线DM折叠(如图2丙)，此时点G恰好与N点重合．
请你探究：矩形纸片ABCD是否是一张标准纸，请说明理由；

(3)不难发现：将一张标准纸按如图3所示方式一次又一次对开后，所得的矩形纸片都是标准纸，现有一张标准纸ABCD，AB＝1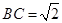，，问第5次对开后所得标准纸的周长是多少？探索并直接写出第2014次对开后所得标准纸的周长．

如图，已知两个共一个顶点的等腰Rt△ABC，Rt△CEF，∠ABC＝∠CEF＝90°，连接AF，M是AF的中点，连接MB、ME．
（1）如图（1），当CB与CE在同一直线上时，求证：MB∥CF；
（2）如图（1），若CB＝a，CE＝2a，求BM，ME的长；
（3）如图（2），当∠BCE＝45°时，求证：BM＝ME．

如图，在Rt△ABC中，∠ACB＝90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连接DE．
（1）证明：DE∥CB；
（2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．

在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB＝5，BC＝6，则CE＋CF的值为(　　)

A．

B．

C．或

D．或

如图，四边形ABCD中，AB＝CD，G，H分别是BC，AD的中点，BA，CD的延长线分别交GH的延长线于点E，F．猜想∠AEH与∠F的关系，并说明理由．

如图所示，在四边形ABCD中，AD∥BC，E是AD上一点，且AE＝3，ED＝2，BC＝15，AB＝8，DC＝6，则AB与CD互相垂直吗？请说明理由．

如图□ABCD中，对角线AC与BD相交于点E，∠AEB＝45°，BD＝2，将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内，若点B的落点记为B′，求DB′的长．

已知：如图1，一次函数的图像与x轴、y轴分别交于点A、B，与函数的图像交于点C，点C的横坐标为－3．

（1） 求点B的坐标；
（2） 若点Q为直线OC上一点，且，求点Q的坐标；
（3） 如图2，点D为线段OA上一点，∠ACD＝∠AOC．点P为x轴负半轴上一点，且点P到直线CD和直线CO的距离相等．
① 在图2中，只利用圆规作图找到点P的位置；
（保留作图痕迹，不得在图2中作无关元素．）
② 求点P的坐标．

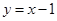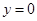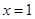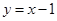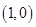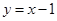我们将使得函数值为零的自变量的值称为函数的零点值，此时的点称为函数的零点．例如，对于函数，令，可得，我们就说1是函数的零点值，点是函数的零点．
已知二次函数．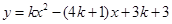
（1）若函数有两个不重合的零点时，求k的取值范围；
（2）若函数的两个零点都是整数点，求整数k的值；
（3）当k<0时，在（2）的条件下，函数的两个零点分别是点A，B（点A在点B的左侧），将二次函数的图象在点A，B间的部分（含点A和点B）向左平移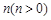个单位后得到的图象记为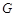，同时将直线向上平移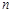个单位．请结合图象回答：当平移后的直线与图象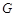有公共点时，求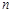的取值范围．

如图，AB是⊙O 的直径，CD是⊙O的一条弦，且CD⊥AB于点E．

（1）求证：∠BCO=∠D；
（2）若CD=，AE=2，求⊙O的半径．

如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，－3），△AB′O′是△ABO关于点A的位似图形，且O′的坐标为（－1，0），则点B′的坐标为________．

在研究相似问题时，甲、乙同学的观点如下：
甲：将边长为3、4、5的三角形按图①的方式向外扩张，得到新三角形，它们的对应边间距均为1，则新三角形与原三角形相似．
乙：将邻边为3和5的矩形按图②的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形不相似．
对于两人的观点，下列说法正确的是(　　)

A．两人都对	B．两人都不对
C．甲对，乙不对	D．甲不对，乙对

如图，晚间小明站在距离路灯5m(即BD＝5m)的地面上，发现他的影子长DF为4m．已知小明的身高为1.6m，如果小明再向远离路灯的方向走4m，则此时小明的影长是多少？