高中数学合情推理和演绎推理试题

先阅读下列不等式的证法，再解决后面的问题：已知，，求证．
证明：构造函数，
因为对一切，恒有≥0，所以≤0，从而得，
（1）若，，请写出上述结论的推广式；
（2）参考上述解法，对你推广的结论加以证明．

对、，运算“”、“”定义为：=，=，则下列各式其中恒成立的是（   ）
　⑴    　　　     ⑵
⑶    　　　   ⑷

A．⑴、⑵、⑶、⑷	B．⑴、⑵、⑶
C．⑴、⑶	D．⑵、⑷

给定整数，证明：存在n个互不相同的正整数组成的集合S，使得对S的任意两个不同的非空子集A，B，数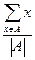
 与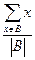 
是互素的合数．（这里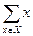与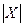分别表示有限数集的所有元素之和及元素个数．）

凸边形中的每条边和每条对角线都被染为n种颜色中的一种颜色．问：对怎样的n，存在一种染色方式，使得对于这n种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形的顶点，且它的3条边分别被染为这3种颜色？

观察以下两个等式：⑴; ⑵，归纳其特点可以获得一个猜想是：                 ．

观察sin²20°+cos²50°+sin20°cos50°
=,sin²15°+cos²45°+sin15°·cos45°=，
写出一个与以上两式规律相同的一个等式        .

在Rt△ABC中，CA⊥CB，斜边AB上的高为h₁，则；类比此性质，如图，在四面体P—ABC中，若PA，PB，PC两两垂直，底面ABC上的高为h，则得到的正确结论为                                   ；

对于定义域为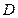的函数，若同时满足：①在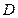内单调递增或单调递减；②存在区间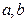，使在上的值域为；那么把函数（）叫做闭函数．
(1) 求闭函数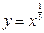符合条件②的区间；
(2) 若是闭函数，求实数的取值范围．

已知 ,猜想的表达式为
                   

如图，圆周上按顺时针方向标有五个点。一只青蛙按顺时针方向绕圆从一个点跳到另一点。若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则跳两个点。该青蛙从这点跳起，经2008次跳后它将停在的点是（　　）

A．

B．

C．

D．

平面向量也叫二维向量，二维向量的坐标表示及其运算可以推广到维向量，维向量可用表示.设,,规定向量与夹角的余弦为.当,时，="            "
A．        B．       C．       D．

出下面类比推理命题（其中Q为有理数集，R为实数集，C为复数集）：
①“若a,b”类比推出“若a,b”；
②“若a,b,c,d”类比推出“若a,b,c,d
则”；
③“若a,b” 类比推出“若a,b”；
其中类比结论正确的个数是  （  ）

A．0

B．1

C．2

D．3

若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x²、值域为{0,4}的“同族函数”共有(   )个.

A． 2

B．3

C．4

D．无数

若平面四边形满足,,则该四边形一定是
A．直角梯形             B．矩形           C．正方形          D．菱形

若存在正整数，使得能被整除，则=