某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形 如图乙所示, 米, 米,在五边形 区域上种植花卉,则大正方形花坛种植花卉的面积 与 的函数图象大致是

A. B.
B.
C. D.
D.
天水某景区商店销售一种纪念品,这种商品的成本价10元 件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于16元 件,市场调查发现,该商品每天的销售量 (件 与销售价 (元 件)之间的函数关系如图所示.
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)求每天的销售利润 (元 与销售价 (元 件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

如图所示,在正方形 和 中, , ,点 、 、 、 在同一直线 上.当点 、 重合时, 以 的速度沿直线 向左开始运动, 秒后正方形 与 重合部分的面积为 .请解答下列问题:
(1)当 秒时,求 的值;
(2)当 秒时,求 的值;
(3)当5秒 秒时,求 与 的函数关系式,并求出 的最大值.
麦积山石窟是世界文化遗产,国家 级旅游景区,中国四大石窟之一.在2018年中国西北旅游营销大会暨旅游装备展上,商家按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按此进价进货、标价销售,商家每天可售出该工艺品100件;若每件工艺品降价1元,则每天可多售出该工艺品4件.问:每件工艺品降价多少元销售,每天获得的利润最大?获得的最大利润是多少元?
某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月(按30天计算),这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第 天 且 为整数)的销售量为 件.
(1)直接写出 与 的函数关系式;
(2)设第 天的利润为 元,试求出 与 之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为 米.
(1)若苗圃园的面积为72平方米,求 ;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出 的取值范围.

某果园有100棵橙子树,平均每棵树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了 棵橙子树.
(1)直接写出平均每棵树结的橙子个数 (个 与 之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
某商店原来平均每天可销售某种水果200千克,每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可多售出20千克.
(1)设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式;
(2)若要平均每天盈利960元,则每千克应降价多少元?
襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为: .
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是 ,则矩形ABCD的面积是( )
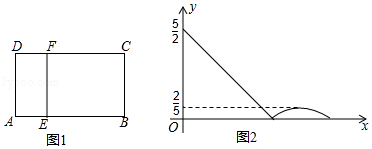
A. B.5C.6D.
当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量 y(本)与销售单价 x(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠 a(0< a≤6)元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求 a的值.
某工厂制作 A, B两种手工艺品, B每件获利比 A多105元,获利30元的 A与获利240元的 B数量相等.
(1)制作一件 A和一件 B分别获利多少元?
(2)工厂安排65人制作 A, B两种手工艺品,每人每天制作2件 A或1件 B.现在在不增加工人的情况下,增加制作 C.已知每人每天可制作1件 C(每人每天只能制作一种手工艺品),要求每天制作 A, C两种手工艺品的数量相等.设每天安排 x人制作 B, y人制作 A,写出 y与 x之间的函数关系式.
(3)在(1)(2)的条件下,每天制作 B不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知 C每件获利30元,求每天制作三种手工艺品可获得的总利润 W(元)的最大值及相应 x的值.
某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨 .据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为1500元;旺季所有的货车每天能全部租出,日租金总收入为4000元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量 y(万件)与销售单价 x(元)之间的关系可以近似地看作一次函数 y=﹣2 x+100
(1)写出每月的利润 L(万元)与销售单价 x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
试题篮
()