初中数学对称式和轮换对称式试题

如图，在平面直角坐标系中完成下列各题：（不写作法，保留作图痕迹）

（1）在图1中作出关于y轴对称的，并写出、、的坐标；
（2）在图2中x轴上画出点，使的值最小．

小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图所示，则电子表的实际时刻是__________．

下列交通标志图案是轴对称图形的是

如图，在平面直角坐标系xoy中，A(-1，5)，B(-1，0)，C(-4，3)。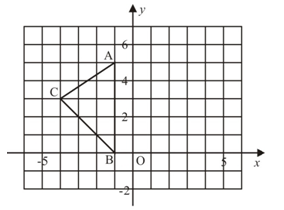

（1）求出△ABC的面积；
（2）在图中作出△ABC关于y轴的对称图形△A₁B₁C₁；
（3）写出点A₁，B₁，C₁的坐标。

如图，已知△ABC的三个顶点的坐标分别为A（﹣6，0）、B（﹣2，3）、C（﹣1，0）．

（1）请直接写出与点B关于坐标原点O的对称点B₁的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°．画出对应的△A′B′C′图形，直接写出点A的对应点A′的坐标；
（3）若四边形A′B′C′D′为平行四边形，请直接写出第四个顶点D′的坐标．

下列手机软件图标中，属于中心对称的是（   ）

如图，△ABC的三个顶点都在方格纸的格点上，其中点A的坐标是（﹣1，0）．现将△ABC绕点A顺时针旋转90°，则旋转后点C的坐标是

A．（2，1）

B．（1，2）

C．（-2，-1）

D．（-2，1）

如图，将△ABC沿直线DE折叠后，使得点B与点A重合．已知AC=5cm，△ADC的周长为17cm，则BC的长为（ ）

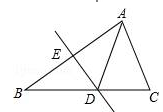
A．7cm

B．10cm

C．12cm

D．22cm

在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是．

（1）将△ABC沿y轴正方向平移3个单位得到△，画出△，并写出点的坐标；
（2）画出△关于y轴对称的△，并写出点的坐标．

点关于轴的对称点的坐标为________________．

下面四个图形分别是节能、节水、绿色食品和低碳标志，在这四个标志中，是轴对称图形的是（   ）

A．

B．

C．

D．

操作与探究
在Rt△ABC中，∠C=90°，AB=5，AC=3，点O是AB的中点，将一块直角三角板ODE的直角顶点绕点O旋转，边OD、OE分别与△ABC的边BC、AC交于点N、M．
（1）如图①，当三角板的一条直角边与AB重合时，点M与点A也重合，
①求此时CN的长；②写出AC²、CN²、BN²满足的数量关系：__________________；

图①
（2）当三角板旋转到如图②所示的位置时，即点M在AC上（不与A、C重合），
①猜想图②中AM²、BN²、MN²满足的数量关系：___________________________；
②说明你得出此结论的理由．

图②
（3）若在三角板旋转的过程中满足CM=CN，请你利用图③，求出此时BN的长．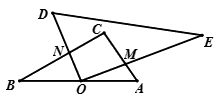

图③

如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．

（1）请你探究∠CEF与∠ADC的数量关系，并证明你的结论；
（2）若EF∥CD，求∠BDC的度数．

如图，OE是∠AOB的平分线，BD⊥OA于点D，AC⊥BO于点C，则关于直线OE对称的三角形共有         对．

开车时，从后视镜中看到后面一辆汽车车牌号的后四位数是“”，则该车号牌的后四位应该是         ．