初中数学对称式和轮换对称式试题

下面有4个汽车标志图案，其中是轴对称图形的有（  ）
     

A．1个

B．2个

C．3个

D．4个

如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）

（1）请画出△ABC关于x轴对称的△A₁B₁C₁，并写出点A₁的坐标；
（2）请画出△ABC绕点B逆时针旋转90°后的△A₂BC₂；
（3）求出（2）中C点旋转到C₂点所经过的路径长（保留根号和π）

下列图形是几家通讯公司的标志，其中既是轴对称图形又是中心对称图形的是（ ）

如图，一段抛物线：y＝－x（x－3）（0≤x≤3），记为C1，它与x轴交于点O，A1；
将C1绕点A1旋转180°得C2，交x 轴于点A2；
将C2绕点A2旋转180°得C3，交x 轴于点A3；
……
如此进行下去，直至得C2015．若P（m，2）在第2015段抛物线C2015上，则m =_________．

如图，点A关于y轴的对称点的坐标是                ．

探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？

如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线成轴对称的△A；
（2）线段被直线                        ；
（3）在直线上找一点P，使PB+PC的长最短，并算出这个最短长度．

下列“数字”图形中，有且仅有一条对称轴的是（  ）

如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（   ）

A．a户最长

B．b户最长

C．c户最长

D．三户一样长

阅读下列材料，然后解答问题．
经过正四边形（即正方形）各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．
如图，正方形ABCD内接于⊙O，⊙O的面积为S₁，正方形ABCD的面积为S₂．以圆心O为顶点作∠MON，使∠MON＝90°．将∠MON绕点O旋转，OM、ON分别与⊙O交于点E、F，分别与正方形ABCD的边交于点G、H．设由OE、OF、及正方形ABCD的边围成的图形（阴影部分）的面积为S．
（1）当OM经过点A时（如图①），则S、S₁、S₂之间的关系为：            （用含S₁、S₂的代数式表示）；
（2）当OM⊥AB于G时（如图②），则（1）中的结论仍然成立吗？请说明理由；
（3）当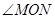旋转到任意位置时（如图③），则（1）中的结论仍然成立吗？请说明理由；

下列图形中，是中心对称图形的是（  ）

如图，将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，D，D′分别是AB，A′B′的中点，且，已知AC=8cm，BC=6cm，求线段DD′的长．

如图所示，在△OAB中，点B的坐标是（0，4），点A的坐标是（3，1）．

（1）画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O₁A₁B₁．
（2）画出△OAB绕点O逆时针旋转90°后的△OA₂B₂，并求出点A旋转到A₂所经过的路径长（结果保留π）．

一个图形无论经过平移还是旋转，有以下说法：
①对应线段平行；
②对应线段相等；
③对应角相等；
④图形的形状和大小都没有发生变化．
其中说法正确的是有          ．

如图所示，将正方形图案绕中心O旋转180°后，得到的图案是