初中数学二次函数在给定区间上的最值试题

下列四个函数图象中，当时，随的增大而增大的是 

在平面直角坐标系中，将二次函数y=2x²的图象向上平移2个单位，所得函数图象的解析式为

A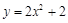．	B．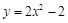
C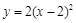．	D．

一个足球从地面上被踢出，它距地面高度y（米）可以用二次函数y=－4．9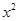+19．6x刻画，其中x（秒）表示足球被踢出后经过的时间．则足球被踢出后到离开地面达到最高点所用的时间是        秒．

已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列4个结论：
①abc＜0；②b＞a+c；③2a-b=0；④b²-4ac＜0．其中正确的结论个数是（   ）

A．1个

B．2个

C．3个

D．4个

如图，直线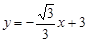与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴交于另一点A，线段BC与抛物线的对称轴l相交于点D，设抛物线的顶点为P，连接AD，线段AD与y轴相交于点E．

（1）求该抛物线的解析式及对称轴；
（2）连结AP，请在y轴正半轴上找一点Q，使Q、C、D为顶点的三角形与△ADP全等，并求出点Q的坐标．将∠CED绕点E顺时针旋转，边EC旋转后与线段BC相交于点M，边ED旋转后与对称轴l相交于点N，若2DM=DN，求点M的坐标．

某种商品的进价为40元/件，以获利不低于25%的价格销售时，商品的销售单价y（元/件）与销售数量x（件）（x是正整数）之间的关系如下表：

x（件）	…	5	10	15	20	…
y（元/ 件）	…	75	70	65	60	…

 
（1）由题意知商品的最低销售单价是      元，当销售单价不低于最低销售价时，y是x的一次函数．y与x的函数关系式是           ．
（2）当销售单价为多少元时，所获销售利润最大，最大利润是多少元？

如表，给出了一个二次函数的一些取值情况：

（1）请在坐标系中（答卷纸上）画出这个二次函数的图象；  
（2）根据图象写出：当0≤y<3时x的取值范围．

二次函数y=x²的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=x²的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积是______．

二次函数y=x²－8x+11的顶点坐标是______．

如图，正三角形ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C
的方向运动，到达点C时停止．设运动时间为x（秒），y＝PC²，则y关于x的函数的图象大致是（   ）

教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）间的
关系为，由此可知铅球推出的距离是（   ）

A．2m

B．8m

C．10m

D．12

如图是二次函数y=ax²+bx+c的部分图象，由图象可知该二次函数的对称轴是（   ）

A．直线x=－1

B．直线x=2

C．直线x=5

D．直线x=0

将抛物线向左平移2个单位后，得到的抛物线的解析式是（ ）

A．	B．
C．	D．

如图，在平面直角坐标系中，顶点为（4，﹣1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧），已知A点坐标为（0，3）．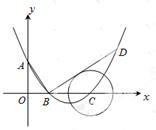

（1）求此抛物线的解析式
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C有怎样的位置关系，并给出证明；
（3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

如图，抛物线与轴交于，两点，与轴交于点，且．

（1）求抛物线的解析式及顶点的坐标；
（2）判断的形状，证明你的结论；
（3）点是轴上的一个动点，当的值最小时，求的值．