初中数学二次函数在给定区间上的最值试题

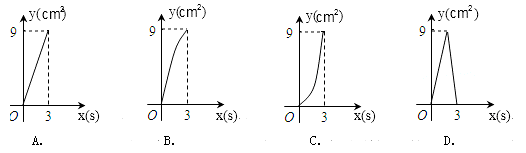
如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=6cm，动点P从点C沿CA，以1cm/s的速度向点A运动，同时动点O从点C沿CB，以2cm/s的速度向点B运动，其中一个动点到达终点时，另一个动点也停止运动．则运动过程中所构成的△CPO的面积y（cm²）与运动时间x（s）之间的函数图象大致是（ ）

已知二次函数y=﹣x²+2x+3，当x≥2时，y的取值范围是（ ）

A．y≥3

B．y≤3

C．y≥4

D．y≤4

函数y=2x²－x－1的图象经过点（    ）             

A．（－1，1）

B．（1 ，1）

C．（0 ，1）

D．（1 ，0 ）

一次函数y=kx-3的图象经过点（1，-2）．
（1）求这个一次函数关系式；
（2）点（2，-1）是否在此函数的图象上？说明理由；
（3）当x为何值时，y≤0？

如图，抛物线经过A（4，0）、B（1，0）、C（0，-2）三点．

（1）求出抛物线的解析式；
（2）在直线AC上方的抛物线上有一动点D，当△ACD的面积最大时，求出点D的坐标；
（3）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

已知抛物线y=ax²＋bx＋c的部分图象如图所示，若y＞0，则x的取值范围是________．

抛物线y =2x²+8x+m与x轴只有一个公共点，则m值为       ．

函数y=a（x-1）²，y=ax+a的图象在同一坐标系的图象可能是（  ）

抛物线向右平移1个单位，再向下平移2个单位，所得到的抛物线是（  ）                                                   

A．y=3（x-1）^2-2	B．y=3（x+1）^2-2
C．y=3（x+1）^2+2	D．y=3（x-1）^2+2

二次函数的图象的对称轴为（  ）

A．

B．

C．

D．

已知抛物线与轴交于点，且．

（1）求抛物线的解析式．
（2）抛物线的对称轴为，与y轴的交点为C，顶点为D，点C关于的对称点为E．是否存在x轴上的点M、y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形
时，求点P的坐标。

为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌
粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．
（1）试求出每天的销售量y（盒）与每盒售价 （元）之间的函数关系式；
（2）当每盒售价定为多少元时，每天销售的利润 （元）最大？最大利润是多少？

请在同一坐标系中画出二次函数①；②的图象。说出两条抛物线的位置关系，指出②的开口方向、对称轴和顶点坐标及增减性。

已知点都在二次函数的图象上，则
的大小关系是            ．

如图，二次函数的图象与轴交于，两点，与轴交 于点，且．则下列结论：①②；③；④．其中正确结论的个数是（   ）

A．4

B．3

C．2

D．1