高中数学变量间的相关关系试题

某著名纺织集团为了减轻生产成本继续走高的压力,计划提高某种产品的价格,为此销售部在10月1日至10月5日连续五天对某个大型批发市场中该产品一天的销售量及其价格进行了调查,其中该产品的价格x(元)与销售量y(万件)之间的数据如下表所示:

日期	10月1日	10月2日	10月3日	10月4日	10月5日
价格x(元)	9	9.5	10	10.5	11
销售量 y(万件)	11	10	8	6	5

已知销售量y与价格x之间具有线性相关关系,其回归直线方程为:=-3.2x+,若该集团提高价格后该批发市场的日销售量为7.36万件,则该产品的价格约为(　　)
(A)14.2元        (B)10.8元
(C)14.8元        (D)10.2元

已知一组观测值具有线性相关关系,若对于=x+,求得=0.51,=61.75,=38.14,则线性回归方程为(　　)

A．=0.51x+6.65	B．=6.65x+0.51
C．=0.51x+42.30	D．=42.30x+0.51

变量X与Y相对应的一组数据为(10,1),(11.3,2),
(11.8,3),(12.5,4),(13,5),变量U与V相对应的一组数据为(10,5),(11.3,4),
(11.8,3),(12.5,2),(13,1).r₁表示变量Y与X之间的线性相关系数,r₂表示变量V与U之间的线性相关系数,则(　　)

A．r2<r1<0	B．0<r2<r1
C．r2<0<r1	D．r2=r1

下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程＝3－5x，变量x增加一个单位时，y平均增加5个单位；
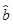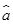③线性回归方程＝x＋必过(，)；
④在一个2×2列联表中，由计算得K²＝13.079，则有99%的把握确认这两个变量间有关系．
其中错误的个数是(　　)
本题可以参考独立性检验临界值表：

P(K^2≥k)	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

A．0   B．1  C．2  D．3

一家商场为了确定营销策略，进行了投入促销费用x和商场实际销售额y的试验，得到如下四组数据．

投入促销费用x(万元)	2	3	5	6
商场实际营销额y(万元)	100	200	300	400

(1)在下面的直角坐标系中，画出上述数据的散点图，并据此判断两个变量是否具有较好的线性相关性；

(2)求出x，y之间的回归直线方程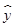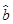＝x＋；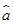
(3)若该商场计划营销额不低于600万元，则至少要投入多少万元的促销费用？

观测两个相关变量，得到如下数据：

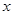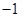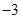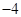						5	4	3	2	1
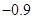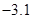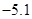						5	4.1	2.9	2.1	0.9

则两变量之间的线性回归方程为（    ）
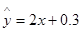A．    B．   C．   D．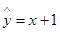

四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
①y与x负相关且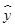＝2.347x－6.423；
②y与x负相关且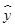＝－3.476x＋5.648；
③y与x正相关且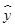＝5.437x＋8.493；
④y与x正相关且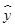＝－4.326x－4.578.
其中一定不正确的结论的序号是(　　)

A．①②	B．②③
C．③④	D．①④

四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
①y与x负相关且＝2.347x－6.423；
②y与x负相关且＝－3.476x＋5.648；
③y与x正相关且＝5.437x＋8.493；
④y与x正相关且＝－4.326x－4.578.
其中一定不正确的结论的序号是(　　)．

A．①②

B．②③

C．③④

D．①④

以下正确命题的个数为（  ）
①命题“存在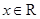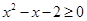，”的否定是：“不存在，”；
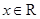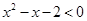②函数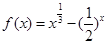的零点在区间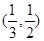内；
③ 函数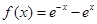的图象的切线的斜率的最大值是；
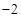④线性回归直线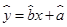恒过样本中心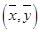，且至少过一个样本点.

A．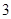

B．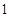

C．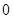

D．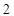

某产品的广告费用x与销售额y的统计数据如下表：

广告费用x(万元)	3	4	5	6
销售额y(万元)	25	30	40	45

根据上表可得回归方程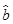＝x＋中的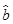为7.据此模型预报广告费用为10万元时销售额为________(万元)．

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验.根据收集到的数据（如下表），由最小二乘法求得回归直线方程，表中有一个数据模糊不清，请你推断出该数据的值为(    )

A．75

B．62

C．68

D．81

某小卖部销售一品牌饮料的零售价（元/瓶）与销量（瓶）的关系统计如下：

零售价（元/瓶）
销量（瓶）	50	44	43	40	35	28

已知的关系符合线性回归方程，其中，．当单价为元时，估计该小卖部销售这种品牌饮料的销量为   （   ）
A．              B．              C．              D．

某车间加工零件的数量与加工时间的统计数据如表：

零件数（个）	10	20	30
加工时间（分钟）	21	30	39

现已求得上表数据的回归方程中的值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为（　　）
A、84分钟          B、94分钟           C、102分钟        D、112分钟

四名同学根据各自的样本数据研究变量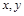之间的相关关系，并求得回归直线方程，
分别得到以下四个结论：
① y与x负相关且； 
② y与x负相关且；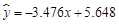
③ y与x正相关且； 
④ y与x正相关且.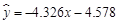
其中一定不正确的结论的序号是__________.

A．①②

B．②③

C．③④

D．①④

已知两个变量x，y之间具有线性相关关系，试验测得(x，y)的四组值分别为(1,2)，(2,4)，(3,5)，(4,7)，则y与x之间的回归直线方程为(　　)

A．y＝0.8x＋3	B．y＝－1.2x＋7.5
C．y＝1.6x＋0.5	D．y＝1.3x＋1.2