高中数学变量间的相关关系试题

．已知x，y的取值如下表：如果y与x成线性相关，且线性回归方程为=       

A．

B．

C．

D．

由下表可计算出变量的线性回归方程为（　　）

	5	4	3	2	1
	2	1.5	1	1	0.5

 
A．             B．
C．           D．

已知的值如表所示：

	2	3	4
	5	4	6

如果与呈线性相关且回归直线方程为，则 (       )
A．             B．             C．       D．

（本小题满分12分）品厂为了检查甲、乙两条自动包装流水线的生产情况，在这两条
流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]
的产品为合格品，否则为不合格品，表1是甲流水线样本频数分布表，图1是乙流水线样
本的频率分布直方图。
某食
（1）若检验员不小心将甲、乙两条流水线生产的重量值在（510，515]的产品放在了一起，
然后又随机取出3件产品，求至少有一件是乙流水线生产的产品的概率；
（2）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。

	甲流水线	乙流水线	合 计
合格品	a=	b=
不合格品	c=	d=
合 计			n=

 

已知某车间加工零件的个数与所花费时间之间的线性回归方程为,
则加工600个零件大约需要的时间为

A．

B．

C．

D．

为了比较注射 $A,B$ 两种药物后产生的皮肤疱疹的面积，选200只家兔做实验，将这200只家兔随即地分成两组。每组100只，其中一组注射药物 $A$ ，另一组注射药物 $B$ .下表1和表2分别是注射药物A和药物B后的实验结果。（疱疹面积单位： $m{m}^2$ ）
表1：注射药物 $A$ 后皮肤疱疹面积的频数分布表

表2：注射药物 $B$ 后皮肤疱疹面积的频数分布表

（Ⅰ）完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；

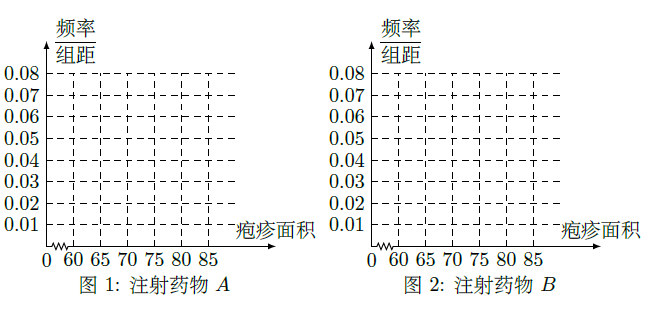
（Ⅱ）完成下面 $2\times 2$ 列联表，并回答能否有99.9％的把握认为"注射药物 $A$ 后的疱疹面积与注射药物 $B$ 后的疱疹面积有差异".
表3：

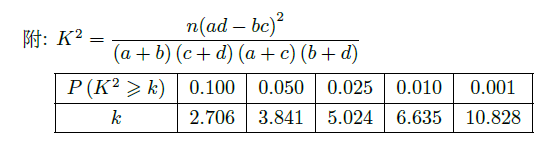
在数学趣味知识培训活动中，甲、乙两名学生的5次培训成绩如下茎叶图所示：

（1）从甲、乙两人中选择1人参加数学趣味知识竞赛，你会选哪位？请运用统计学的知识说明理由；
（2） 从乙的5次培训成绩中随机选择2个，试求选到121分的概率．

为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：

收入 $x$（万元）	8.2	8.6	10.0	11.3	11.9
支出 $y$（万元）	6.2	7.5	8.0	8.5	9.8

根据上表可得回归直线方程 $\hat{y}=\hat{b}x+\hat{a}$ ，其中 $\hat{b}=0.76,\hat{a}=\overline{y}-\hat{b}\overline{x}$，据此估计，该社区一户收入为15万元家庭年支出为（    ）

A．

11.4万元

B．

11.8万元

C．

12.0万元

D．

12.2万元

某班的全体学生参加消防安全知识竞赛，成绩的频率分布直方图如图，数据的分组依次为：
[20，40），[40，60），[60，80），[80，100]．若低于60分的人数是15，则该班的学生人数是       ．

由某种设备的使用年限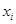（年）与所支出的维修费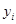（万元）的数据资料算得如下结果，，，，.
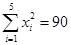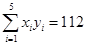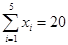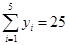（1）求所支出的维修费y对使用年限x的线性回归方程；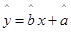
（2）①判断变量x与y之间是正相关还是负相关；
②当使用年限为8年时，试估计支出的维修费是多少.
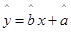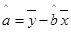（附：在线性回归方程中，），，其中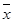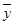，为样本平均值.)

由于工业化城镇化的推进，大气污染日益加重，空气质量逐步恶化，雾霾天气频率增大，大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关，在某医院心血管科随机的对入院50位进行调查得到了如下列联表：问有多大的把握认为是否患心脏病与性别有关. 答：．

A．95%

B．99%

C．99.5%

D．99.9%

	患心脏病	不患心脏病	合计
男	20	5	25
女	10	15	25
合计	30	20	50

 
参考临界值表：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
K	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式： 其中n =" a" + b + c + d）．

假设关于某设备的使用年限和所支出的维修费用（万元），有如下的统计资料：

使用年限	2	3	4	5	6
维修费用	2．2	3．8	5．5	6．5	7．0

 
若由资料知道对呈线性相关关系．
附：
试求：
（1）线性回归方程的回归系数．
（2）估计使用年限为10年时，维修费用是多少？

设有一个直线回归方程为，则变量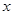增加一个单位（   ）

A．y平均增加 1．5 个单位

B．y 平均增加 2 个单位

C．y 平均减少 1．5 个单位

D．y 平均减少 2 个单位

已知呈线性相关关系的变量，之间的关系如下表所示，则回归直线一定过点（  ）

A．	B．
C．	D．

某池塘中野生水葫芦的面积与时间的函数关系的图象，如图所示．假设其关系为指数函数，并给出下列说法：

①此指数函数的底数为；
②在第个月时，野生水葫芦的面积就会超过；
③野生水葫芦从蔓延到只需个月；
④设野生水葫芦蔓延到，，所需的时间分别为，，，则有；
⑤野生水葫芦在第到第个月之间蔓延的平均速度等于在第到第个月之间蔓延的平均速度．
其中正确的说法有         ．（请把正确说法的序号都填在横线上）