高中数学变量间的相关关系试题

如果在一次试验中，测得()的四组数值分别是

	1	2	3	4
	3	3.8	5.2	6

 
根据上表可得回归方程，据此模型预报当为5时，的值为（  ）
A．6.9         B．7.1       C．7.04         D．7.2

如果随机变量ξ～B（n，p），且Eξ=7，Dξ=6，则P等于_________ ．

已知变量和满足关系，变量与正相关． 下列结论中正确的是（）

A．	与 负相关， 与 负相关
B．	与 正相关， 与 正相关
C．	与 正相关， 与 负相关
D．	与 负相关， 与 正相关

已知x与y之间的一组数据如下，则y与x的线性回归方程为y=bx+a，必过点         ．

x	1	1	2	4
y	1	4	5	6

 

以下是某地搜集到的新房屋的销售价格（万元）和房屋的面积（）的数据 ，若由资料可知对呈线性相关关系。

试求:（1）线性回归方程；
（2）根据（1）的结果估计当房屋面积为时的销售价格.
参考公式：

某数学兴趣小组有男女生各名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位：分).已知男生数据的中位数为，女生数据的平均数为.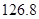
（1）求，的值；
（2）现从成绩高于分的同学中随机抽取两名同学，求抽取的两名同学恰好为一男一女的概率.

某车间加工零件的数量与加工时间的统计如下表：

零件数（个）	10	20	30
加工时间（分钟）	21	30	39

现已求得上表数据的回归方程中的值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为（   ）.
A.84分钟      B.94分钟          C.102分钟          D.112分钟

某产品的广告费用x与销售额y的统计数据如下表：

广告费用x（万元）	4	2	3	5
销售额y（万元）	49	26	39	58

 
根据上表可得回归方程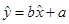中的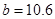，据此模型预报广告费用为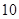万元时销售额为（   ）．
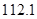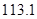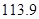A．万元     B．万元       C．万元         D．万元

下表是降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗（吨标准煤）的几组对应数据，根据表中提供的数据，求出关于的线性回归方程：，那么表中的值为(     )

A．3

B．3.15

C．4.5

D．4

为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：

收入 $x$（万元）	8.2	8.6	10.0	11.3	11.9
支出 $y$（万元）	6.2	7.5	8.0	8.5	9.8

根据上表可得回归直线方程 $\hat{y}=\hat{b}x+\hat{a}$ ，其中 $\hat{b}=0.76,\hat{a}=\overline{y}-\hat{b}\overline{x}$，据此估计，该社区一户收入为15万元家庭年支出为（    ）

A．

11.4万元

B．

11.8万元

C．

12.0万元

D．

12.2万元

根据如下样本数据

	3	4	5	6	7	8
	4.0	2.5	-0.5	0.5	-2.0	-3.0

得到的回归方程为,则（）

A．

B．

C．

D．

某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，其可见部分如下，据此解答如下问题：
 
（1）计算频率分布直方图中[80,90)间的矩形的高；
（2）若要从分数在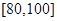之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份试卷的分数在之间的概率；
（3）根据频率分布直方图估计这次测试的平均成绩．

某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：

	2	3	4	5	6
	2.2	3.8	5.5	6.5	7.0

 
已知，，
(1)在下面坐标系中画出散点图；

(2)计算，，并求出线性回归方程；
(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?

假设关于某设备的使用年限和所支出的维修费用（万元），有如下的统计资料：

使用年限	2	3	4	5	6
维修费用	2．2	3．8	5．5	6．5	7．0

 
若由资料知道对呈线性相关关系．
附：
试求：
（1）线性回归方程的回归系数．
（2）估计使用年限为10年时，维修费用是多少？

设有一个直线回归方程为，则变量增加一个单位（   ）

A．y平均增加 1．5 个单位

B．y 平均增加 2 个单位

C．y 平均减少 1．5 个单位

D．y 平均减少 2 个单位