高中数学变量间的相关关系试题

观察下列关于两个变量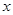和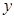的三个散点图，它们从左到右的对应关系依次为（  ）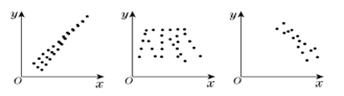

A．正相关、负相关、不相关	B．负相关、不相关、正相关
C．负相关、正相关、不相关	D．正相关、不相关、负相关

已知与之间的一组数据，已求得关于与的线性回归方程为，则的值为（   ）

	0	1	2	3
		3	5.5	7

A．     B．     C．     D．

一个物体的运动方程为其中的单位是米，的单位是秒， 那么物体在秒末的瞬时速度是（   ）

A．米/秒

B．米/秒

C．米/秒

D．米/秒

已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为(　　)

A．=1.23x+4

B．=1.23x+5

C．=1.23x+0.08

D．=0.08x+1.23

调查了某地若干户家庭的年收x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，井由调查数据得到y对x的回归直线方程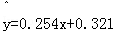．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加      万元．

对具有线性相关关系的变量和，测得一组数据如下：

x	2	4	5	6	8
y	30	40	60	50	70

 
若已求得它们的回归方程的斜率为6．5，则这条直线的回归方程为                  ．

下面是2×2列联表:

	y1	y2	总计
x1	a	21	73
x2	22	25	47
总计	b	46	120

则表中a,b的值分别为(　　)
(A)94,72        (B)52,50
(C)52,74        (D)74,52

已知的取值如表所示

	2	3	4
	6	4	5

 
如果线性相关，且线性回归方程为，则的值为（ ）
A．    B．    C．    D．

在研究硝酸钠的可溶性程度时,在不同的温度下观测它在水中的溶解度,得观测结果如下:

温度(x)	0	10	20	50	70
溶解度(y)	66.7	76.0	85.0	112.3	128.0

则由此得到的回归直线的斜率是　　　　　　.

对一些城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查后知,y与x具有相关关系,满足回归方程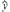=0.66x+1.562.若某被调查城市的居民人均消费水平为7.675(千元),则可以估计该城市人均消费额占人均工资收入的百分比约为　　　　%(结果保留两个有效数字).

四名同学根据各自的样本数据研究变量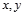之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
①y与x负相关且；
②y与x负相关且；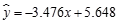
③y与x正相关且；
④y与x正相关且．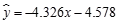
其中一定不正确的结论的序号是 （  ）

A．①②

B．②③

C．③④

D．①④

对有线性相关关系的两个变量建立的回归直线方程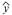=+x中,回归系数(　　)

A．不能小于0	B．不能大于0
C．不能等于0	D．只能小于0

某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：

日  期	1月10日	2月10日	3月10日	4月10日	5月10日	6月10日
昼夜温差(°C)	10	11	13	12	8	6
就诊人数(个)	22	25	29	26	16	12

该兴趣小组确定的研究方案是：先从这六组数据中选取组，用剩下的组数据求线性回归方程，再用被选取的组数据进行检验．
（Ⅰ）求选取的组数据恰好是相邻两个月的概率；
（Ⅱ）若选取的是月与月的两组数据，请根据至月份的数据，求出关于的线性回归方程；（其中）
（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人，则认为得到的线性回归方程是理想的．试问该小组所得线性回归方程是否理想？

对于给定的两个变量的统计数据,下列说法正确的是(　　)

A．都可以分析出两个变量的关系

B．都可以用一条直线近似地表示两者的关系

C．都可以作出散点图

D．都可以用确定的表达式表示两者的关系

已知的取值如下表所示，若与线性相关，且，则（   ）

A．         B．        C．      D．[