经统计,某地的财政收入
与支出
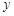满足的线性回归模型是
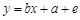(单位:亿元),其中
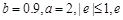为随机误差,如果今年该地区财政收入10亿元,则年支出预计不超出( )
| A．10亿 | B．11亿 | C．11.5亿 | D．12亿 |
对于给定的两个变量的统计数据,下列说法正确的是( )
| A．都可以分析出两个变量的关系 |
| B．都可以用一条直线近似地表示两者的关系 |
| C．都可以作出散点图 |
| D．都可以用确定的表达式表示两者的关系 |
下面两个变量间的关系不是函数关系的是( )
| A．正方体的棱长与体积 |
| B．角的度数与它的正弦值 |
| C．单位产量为常数时,土地面积与粮食总产量 |
| D．日照时间与水稻亩产量 |
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了
至
月份每月
号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
| 日 期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
昼夜温差 (°C) |
10 |
11 |
13 |
12 |
8 |
6 |
就诊人数 (个) |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是：先从这六组数据中选取
组，用剩下的
组数据求线性回归方程，再用被选取的组数据进行检验．
（Ⅰ）求选取的组数据恰好是相邻两个月的概率；
（Ⅱ）若选取的是月与月的两组数据，请根据至
月份的数据，求出关于的线性回归方程
；（其中
）
（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人，则认为得到的线性回归方程是理想的．试问该小组所得线性回归方程是否理想？
（本小题满分12分）为了分析某个高中学生的学习状态，对其下一阶段的学习提供指导性建议。现对他前7次考试的数学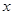成绩
、物理成绩
进行分析。下面是该生7次考试的成绩，可见该生的物理成绩与数学成绩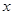是线性相关的：
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
（1）求物理成绩与数学成绩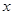的回归直线方程
;
（2）若该生的物理成绩达到115分，请你估计他的数学成绩大约是多少？
参考公式：
， 
参考数据：
，
如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图，现已知年龄 在[30，35），[35，40），[40，45]的上网人数呈现递减的等差数列，则年龄在[35，40）的频率（ ）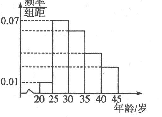
| A．0．04 |
| B．0．06 |
| C．0．2 |
| D．0．3 |
在一组样本数据 的散点图中,若所有样本点 都在直线 上，则这组样本数据的样本相关系数为（）
| A． | －1 | B． | 0 | C． | D． | 1 |
已知x、y之间的一组数据如下：
| x |
0 |
1 |
2 |
3 |
| y |
8 |
2 |
6 |
4 |
则线性回归方程
所表示的直线必经过点（ ）
A．（0，0） B．（1.5,5） C．（4,1.5） D．（2,2）
某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )
A． ＝－10x＋200 |
B．＝10x＋200 |
| C．＝－10x－200 |
D．＝10x－200 |
某农场给某种农作物施肥量x(单位：吨)与其产量y(单位：吨)的统计数据如下表：
| 施肥量x |
2 |
3 |
4 |
5 |
| 产量y |
26 |
39 |
49 |
54 |
根据上表，得到回归直线方程
＝9.4x＋
，当施肥量x＝6时，该农作物的预报产量是________．
甲，乙，丙，丁四位同学各自对A，B两变量的线性相关试验，并用回归分析方法分别求得相关系数r如表：
| |
甲 |
乙 |
丙 |
丁 |
| r |
0.82 |
0.78 |
0.69 |
0.85 |
则这四位同学的试验结果能体现出A，B两变量有更强的线性相关性的是（ ）.
A．甲 B．乙 C．丙 D．丁
某产品的广告费用与销售额的统计数据如下表：
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程y=bx+a中的b为9.4，据此模型预报广告费用为6万元时销售额为（ ）
A．63.6万元 B．65.5万元 C． 67.7万元 D．72.0万元
试题篮
()
粤公网安备 44130202000953号
的取值如下表所示，若
与
线性相关，且
，则
（ ）
C．
D．
[
（件）与销售价格
（元/件）负相关，则其回归方程可能是（ ）
