经过对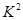 的统计量的研究,得到了若干个临界值,当
的统计量的研究,得到了若干个临界值,当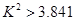 时,我们
时,我们
A.有95%的把握认为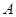 与 与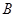 有关. 有关. |
B.有99%的把握认为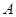 与 与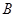 有关 有关 |
C.没有充分理由说事件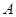 与 与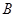 有关 有关 |
D.有97.5%的把握认为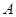 与 与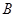 有关 有关 |
某种产品的广告费用支出 万元与销售额
万元与销售额 万元之间有如下的对应数据:
万元之间有如下的对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
20 |
30 |
50 |
50 |
70 |
(1)根据上表提供的数据,求出y关于x的线性回归方程;
(2)据此估计广告费用为10万元时,所得的销售收入.
( ,
,
 )
)
根据一组样本数据(x1,y1),(x2,y2),…,(xn,yn)的散点图分析存在线性相关关系,求得其回归方程 =0.85x-85.7,则在样本点(165,57)处的残差为( )
=0.85x-85.7,则在样本点(165,57)处的残差为( )
| A.54.55 | B.2.45 | C.3.45 | D.111.55 |
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额(x)/千万元 |
3 |
5 |
6 |
7 |
9 9 |
| 利润额(y)/百万元 |
2 |
3 |
3 |
4 |
5 |
(1)画出销售额和利润额的散点图.(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程.
已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )
A. =1.23x+4 =1.23x+4 |
B. =1.23x+5 =1.23x+5 |
C. =1.23x+0.08 =1.23x+0.08 |
D. =0.08x+1.23 =0.08x+1.23 |
根据如图样本数据得到的回归方程为 =bx+a,若样本点的中心为
=bx+a,若样本点的中心为 .则当x每增加1个单位时,y就( )
.则当x每增加1个单位时,y就( )

| A.增加1.4个单位 | B.减少1.4个单位 |
| C.增加7.9个单位 | D.减少7.9个单位 |
四名同学根据各自的样本数据研究变量 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
① 与
与 负相关且
负相关且 ; ②
; ② 与
与 负相关且
负相关且 ;
;
③ 与
与 正相关且
正相关且 ; ④
; ④ 与
与 正相关且
正相关且 .
.
其中一定不正确的结论的序号是( )
| A.①② | B.②③ | C.③④ | D.①④ |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
已知有线性相关关系的两个变量建立的回归直线方程为 ,方程中的回归系数
,方程中的回归系数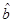 ( )
( )
| A.可以小于0 | B.只能大于0 | C.可以为0 | D.只能小于0 |
为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:
| |
理科 |
文科 |
| 男 |
13 |
10 |
| 女 |
7 |
20 |
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.
根据表中数据,得到k= ≈4.844.
≈4.844.
则认为选修文科与性别有关系出错的可能性为________.
已知x与y之间的一组数据(如表所示):则关于y与x的线性回归方程y=bx+a必过定点( )
| A.(2,2) | B.(1.5,0) | C.(1,2) | D.(1.5,4) |
某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元).
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
t |
70 |
根据上表提供的数据,求出y关于x的线性回归方程为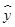 =6.5x+17.5,则表中t的值为________.
=6.5x+17.5,则表中t的值为________.
已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程 =
= x+
x+ ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
试题篮
()