经过对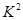 的统计量的研究,得到了若干个临界值,当
的统计量的研究,得到了若干个临界值,当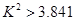 时,我们
时,我们
A.有95%的把握认为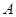 与 与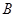 有关. 有关. |
B.有99%的把握认为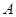 与 与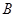 有关 有关 |
C.没有充分理由说事件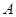 与 与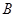 有关 有关 |
D.有97.5%的把握认为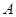 与 与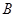 有关 有关 |
某种产品的广告费用支出 万元与销售额
万元与销售额 万元之间有如下的对应数据:
万元之间有如下的对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
20 |
30 |
50 |
50 |
70 |
(1)根据上表提供的数据,求出y关于x的线性回归方程;
(2)据此估计广告费用为10万元时,所得的销售收入.
( ,
,
 )
)
已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程 =
= x+
x+ ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
某产品的广告费用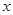 与销售额
与销售额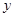 的统计数据如下表:
的统计数据如下表:
广告费用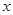 (万元) (万元) |
4 |
2 |
3 |
5 |
销售额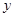 (万元) (万元) |
49 |
26 |
39 |
54 |
根据上表数据预计广告费用为6万元时,销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
用餐时客人要求:将温度为 、质量为
、质量为 的同规格的某种袋装饮料加热至
的同规格的某种袋装饮料加热至 .服务员将
.服务员将 袋该种饮料同时放入温度为
袋该种饮料同时放入温度为 、质量为
、质量为 的热水中,
的热水中, 分钟后立即取出.设经过
分钟后立即取出.设经过 分钟饮料与水的温度恰好相同,此时,
分钟饮料与水的温度恰好相同,此时, 该饮料提高的温度
该饮料提高的温度 与
与 水降低的温度
水降低的温度 满足关系式
满足关系式 ,则符合客人要求的
,则符合客人要求的 可以是( )
可以是( )
A. |
B. |
C. |
D. |
在2013年3月15日这天,郑州市物价部门对本市5家商场某商品一天的销售量及其价格进行了调查,5家商场某商品的销售价格x(元)与销售量y(件)之间的一组数据如下表:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
作出散点图,可知销售量y与价格x之间具有线性相关关系,其线性回归方程是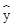 =-3.2x+
=-3.2x+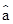 则实数
则实数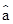 的值是________.
的值是________.
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量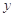 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
为了调查某地居民的年收入x(单位:万元)和年饮食支出y(单位:万元)之间的关系,用分层抽样的方法从该地调查了若干户家庭,调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程为=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出增加________万元.
假设学生在初一和初二数学成绩是线性相关的,若10个学生初一(x)和初二(y)数学分数如下:
| x |
74 |
71 |
72 |
68 |
76 |
73 |
67 |
70 |
65 |
74 |
| y |
76 |
75 |
71 |
70 |
76 |
79 |
65 |
77 |
62 |
72 |
则初一和初二数学分数间的回归方程是 ( ).
A.  =1.218 2x-14.192 B.
=1.218 2x-14.192 B. =14.192x+1.218 2
=14.192x+1.218 2
C.  =1.218 2x+14.192 D.
=1.218 2x+14.192 D.  =14.192x-1.218 2
=14.192x-1.218 2
已知有线性相关关系的两个变量建立的回归直线方程为 ,方程中的回归系数
,方程中的回归系数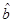 ( )
( )
| A.可以小于0 | B.只能大于0 | C.可以为0 | D.只能小于0 |
下列反映两个变量的相关关系中,不同于其它三个的是
| A.名师出高徒 | B.水涨船高 | C.月明星稀 | D.登高望远 |
试题篮
()