高中数学变量间的相关关系试题

某产品在某零售摊位的零售价x（单位：元）与每天的销售量y（单位：个）的统计资料如下表所示：由上表可得回归直线方程中的，据此模型预测零售价为15元时，每天的销售量为（   ）

A．51个

B．50个

C．49个

D．48个

对“四地六校”的高二年段学生是爱好体育还是爱好文娱进行调查，共调查了40人，其中男生25人，女生15人。男生中有15人爱好体育，另外10人爱好文娱。女生中有5人爱好体育，另外10人爱好文娱；
（1）根据以上数据制作一个2×2的列联表；
（2）在多大的程度上可以认为性别与是否爱好体育有关系？
附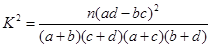： （此公式也可写成）
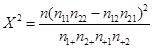参考数据：

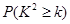	0.25	0.15	0.10	0.05	0.025
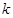	1.323	2.072	2. 706	3. 841	5. 024

 

某种产品的广告费支出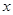（单位：万元）与销售额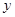（单位：万元）之间的线性回归方程为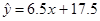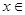，{2,4,5,6,8}，则平均销售额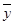为（   ）

A． 6.5

B． 17.5

C． 50

D． 40

对具有线性相关关系的变量x、y有观测数据(x_i，y_i)(i＝1,2，…，10)，它们之间的线性回归方程是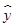＝3x＋20，若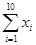＝18，则＝________.

某商品销售量y（件）与销售价格（元/件）负相关，则其回归方程可能是(  )

A．	B．
C．	D．

假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

若由资料可知y对x呈线性相关关系。试求：
（1）线性回归方程；        
（2）估计使用年限为10年时，维修费用是多少？

在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.
（1）根据以上数据建立一个2×2的列联表；
（2）判断性别与休闲方式是否有关系.

下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程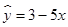，变量x增加一个单位时，y平均增加5个单位；
③线性回归直线方程必过；
④在一个2×2列联表中，由计算得K²=13．079，则有99%的把握确认这两个变量间有关系；
其中错误的个数是（ ）     

A．0

B．1

C．2

D．3

在一组样本数据的散点图中，若所有样本点都在直线上，则这组样本数据的样本相关系数为_______.

某城市近10年居民的年收入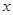与支出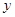之间的关系大致符合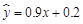（单位：亿元），预计今年该城市居民年收入为20亿元，则今年支出估计是        亿元.

甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性做实验，并用回归分析方法分别求得相关系数r与残差平方和m如下表：

	甲	乙	丙	丁
R	0．82	0．78	0．69	0．85
M	106	115	124	103

 
则哪位同学的实验结果体现A、B两变量有更强的线性相关关系．
A．甲              B．乙            C．丙               D．丁

为了解某班关注NBA是否与性别有关，对本班48人进行了问卷调查得到如下的列联表：

	关注NBA	不关注NBA	合计
男生		6
女生	10
合计			48

已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为.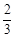
（1）请将上面的表补充完整（不用写计算过程），并判断是否有95%的把握认为关注NBA与性别有关？说明你的理由.
（2）现记不关注NBA的6名男生中某两人为a,b，关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查，求：至少有一人不关注NBA的被选取的概率。
下面的临界值表，供参考

P（K^2≥k）	0.10	0.05	0.010	0.005
K	2.706	3.841	60635	7.879

(参考公式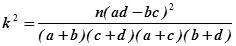：)其中n=a+b+c+d

对具有线性相关关系的变量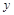，测得一组数据如下表：

x	2	4	5	6	8
y	20	40	60	80	100

根据上表，利用最小二乘法得到它们的回归直线方程为.据此模型预测时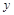，的估计值为（   ）
A. 320       B. 320.5    C. 322.5       D. 321.5

一名小学生的年龄和身高（单位：cm）的数据如下表：

由散点图可知，身高与年龄之间的线性回归方程为，则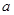的值为（ ）

A．65

B．74

C．56

D．47

下列反映两个变量的相关关系中，不同于其它三个的是

A．名师出高徒

B．水涨船高

C．月明星稀

D．登高望远