假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
| x |
2 |
3 |
4 |
5 |
6 |
| y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知y对x呈线性相关关系。试求:
(1)线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
已知x,y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且  =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80
在10支罐装饮料中,有2支是不合格产品,质检员从这10支饮料中抽取2支进行检验。
(Ⅰ)求质检员检验到不合格产品的概率;
(Ⅱ)若把这10支饮料分成甲、乙两组,对其容量进行测量,数据如下表所示(单位:ml):
| 甲 |
257 |
269 |
260 |
261 |
263 |
| 乙 |
258 |
259 |
259 |
261 |
263 |
请问哪组饮料的容量更稳定些?并说明理由.
已知变量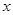 与
与 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,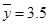 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.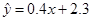 |
B.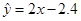 |
C.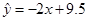 |
D.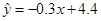 |
为了考察两个变量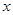 和
和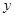 之间的线性相关性,甲、乙两同学各自独立地做
之间的线性相关性,甲、乙两同学各自独立地做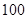 次和
次和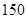 次试验,并且利用线性回归方法,求得回归直线分别为
次试验,并且利用线性回归方法,求得回归直线分别为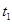 和
和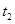 ,已知两个人在试验中发现对变量
,已知两个人在试验中发现对变量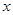 的观测值的平均值都是
的观测值的平均值都是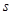 ,对变量
,对变量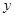 的观测值的平均值都是
的观测值的平均值都是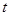 ,那么下列说法正确的是()
,那么下列说法正确的是()
A.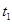 和 和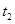 有交点 有交点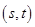 |
B.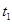 和 和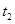 相交,但交点不是 相交,但交点不是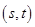 |
C.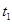 和 和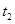 必定重合 必定重合 |
D.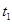 和 和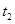 必定不重合 必定不重合 |
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x |
2 |
3 |
4 |
5 |
6 |
| 维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)画出散点图;
(2)若线性相关,则求出回归方程 ;
;
(3)估计使用年限为10年时,维修费用是多少?
(参考公式: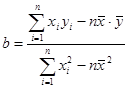 ,
,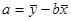 )
)
在下列各量之间,存在相关关系的是 ( )
①正方体的体积与棱长之间的关系; ②一块农田的水稻产量与施肥量之间的关系;
③人的身高与年龄之间的关系; ④家庭的支出与收入之间的关系;
⑤某户家庭用电量与电价之间的关系。
| A.②③ | B.③④ | C.④⑤ | D.②③④ |
利用独立性检验来判断两个分类变量X和Y是否有关系,通过查阅下表来确定“X和Y有关系”的可信度.为了调查用电脑时间与视力下降是否有关系,现从某地网民中抽取100位居民进行调查.经过计算得 ,那么就有_______________%的根据认为用电脑时间与视力下降有关系.
,那么就有_______________%的根据认为用电脑时间与视力下降有关系.
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172cm的高三男生的体重为 ( )
,据此模型预报身高为172cm的高三男生的体重为 ( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
甲、乙两名同学在 次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为
次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
B. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
C. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
D. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
十字路口车流量被定义为单位时间内通过十字路口的车辆数,小张上班经过的某十字路口某时间段内车流量变化近似符合函数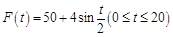 (
(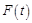 的单位是辆/分,
的单位是辆/分,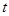 的单位是分),则下列时间段内车流量增加的是
的单位是分),则下列时间段内车流量增加的是
A.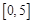 |
B.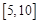 |
C.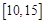 |
D.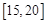 |
以下有关线性回归分析的说法不正确的是
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D.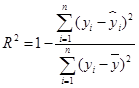 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
某车间加工零件的数量 与加工时间
与加工时间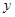 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间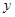 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
试题篮
()