高中数学合情推理和演绎推理选择题

下面使用类比推理正确的是 （       ）
A. “若,则”类推出“若,则”
B. “若”类推出“”
 “若” 类推出“ （c≠0）”
D. “” 类推出“

已知数列：依它的前10项的规律，这个数列的第2010项满足

A．	B．
C．	D．

若大前提是：任何实数的平方都大于0，小前提是：，结论是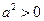：，那么这个演绎推理所得结论错误的原因是：（ ﹡ ）．

A．大前提错误

B．小前提错误

C．推理形式错误

D．大前提小前提都错

观察 ${\left(x^2\right)}^{`}=2x$， ${\left(x^4\right)}^{`}=4x^2$, ${\left(\cos x\right)}^{`}=-\sin x$，由归纳推理可得：若定义在 $R$上的函数 $f\left(x\right)$满足 $f\left(-x\right)=f\left(x\right)$，记 $g\left(x\right)为f\left(x\right)$的导函数，则 $g\left(-x\right)=$（）

A．

$f\left(x\right)$

B．

$-f\left(x\right)$

C．

$g\left(x\right)$

D．

$-g\left(x\right)$

“因对数函数是增函数（大前提），而是对数函数（小前提），所以是增函数（结论）．”上面的推理的错误是

A．大前提错导致结论错	B．小前提错导致结论错
C．推理形式错导致结论错	D．大前提和小前提都错导致结论错

“因为四边形ABCD是矩形，所四边形ABCD的对角线相等”，补充以上推理的大前提是（   ）

A．矩形都是四边形；	B．四边形的对角线都相等；
C．矩形都是对角线相等的四边形；	D．对角线都相等的四边形是矩形

“∵四边形ABCD是矩形，∴四边形ABCD的对角线相等。”补充以上推理的大前提
为（  ）

A．正方形都是对角线相等的四边形	B．矩形都是对角线相等的四边形
C．等腰梯形都是对角线相等的四边形	D．矩形都是对边相等且平行的四边形

演绎推理“因为对数函数是增函数，而函数是对数函数，所以是增函数”所得结论错误的原因是（   ）

A．大前提错误	B．小前提错误
C．推理形式错误	D．大前提和小前提都错误

把下面在平面内成立的结论类比地推广到空间，结论还正确的是                （  ）

A．如果一条直线与两条平行线中的一条相交，则它与另一条也相交．

B．如果一条直线与两条平行线中的一条垂直，则它与另一条也垂直．

C．如果两条直线同时与第三条直线相交，则这两条直线相交．

D．如果两条直线同时与第三条直线垂直，则这两条直线平行．

下面给出了关于复数的四种类比推理：
① 复数的加减法运算，可以类比多项式的加减法运算法则；
② 由向量  的性质 ，可以类比得到复数  的性质 ；
③ 方程 （a 、b 、c ∈ R ）有两个不同实根的条件是,类比可以得到 方程 （a 、b 、c ∈ C）有两个不同复数根的条件是 ；
④ 由向量加法的几何意义，可以类比得到复数加法的几何意义。
其中类比得到的结论正确的是（ *** ）
A．① ③        Ｂ．．② ④       Ｃ．② ③      Ｄ．① ④  

有一段演绎推理：“因为对数函数是减函数；已知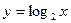是对数函数，所以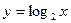是减函数”，结论显然是错误的，这是因为（***）                        

A．大前提错误

B．小前提错误

C．推理形式错误

D．非以上错误

已知直线,平面,且,给出下列命题:①若∥，则m⊥；
②若⊥，则m∥;③若m⊥，则∥；④若m∥，则⊥其中正确命题的个数是（ ）

A．1

B．2

C．3

D．4

由左图中的规律可判断右图问号处的图形应是（    ）
 
                     

由左图中的规律可判断右图问号处的图形应是（        ）
 
                     

以下是面点师一个工作环节的数学模型：如图，在数轴上截取与闭区间对应的线段，对折后（坐标1所对应的点与原点重合）再均匀的拉成一个单位长度的线段，这一过程称为一次操作（例如在第一次操作完成后，原来的坐标变成，原来的坐标变成1，等等）。则区间上（除两个端点外）的点，在第二次操作完成后，恰好被拉到与1重合的点所对应的坐标是，那么在第次操作完成后，恰好被拉到与1重合的点对应的坐标是（    ）

A．为中所有奇数）	B．
C．为中所有奇数）	D．