挪威数学家阿贝尔曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式:
a1b1+a2b2+a3b3+…+anbn=L1(b1-b2)+L2(b2-b3)+L3(b3-b4)+…+Ln-1(bn-1-bn)+Lnbn,其中L1=a1,则
(Ⅰ)L3= ;
(Ⅱ)Ln= .
现有一个关于平面图形的命题:如图所示,同一个平面内有两个变长都是a的正方形,其中一个正方形的某起点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为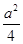 ,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___
,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___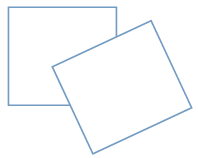
如图的倒三角形数阵满足:⑴第1行的 个数,分别是1,3,5,…,
个数,分别是1,3,5,…, ;⑵ 从第二行起,各行
;⑵ 从第二行起,各行
中的每一个数都等于它肩上的两数之和;⑶数阵共有 行.问:当
行.问:当 时,第32行的第17个数是 ;
时,第32行的第17个数是 ;
给出问题:已知 满足
满足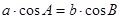 ,试判定
,试判定 的形状.某学生的解答如下:
的形状.某学生的解答如下:
解:(i)由余弦定理可得, ,
,
 ,
,
 ,
,
故 是直角三角形.
是直角三角形.
(ii)设 外接圆半径为
外接圆半径为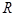 .由正弦定理可得,原式等价于
.由正弦定理可得,原式等价于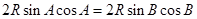

 ,
,
故 是等腰三角形.
是等腰三角形.
综上可知, 是等腰直角三角形.
是等腰直角三角形.
请问:该学生的解答是否正确?若正确,请在下面横线中写出解题过程中主要用到的思想方法;若不正确,请在下面横线中写出你认为本题正确的结果. .
如图的倒三角形数阵满足:⑴ 第1行的 个数,分别是1,3,5,…,
个数,分别是1,3,5,…, ;⑵ 从第二行起,各行中的每一个数都等于它肩上的两数之和;⑶ 数阵共有
;⑵ 从第二行起,各行中的每一个数都等于它肩上的两数之和;⑶ 数阵共有 行.问:当
行.问:当 时,第32行的第17个数是 ;
时,第32行的第17个数是 ;
已知等边三角形ABC的高为 ,它的内切
,它的内切 圆半径为
圆半径为 ,则
,则 ,由此类比得:已知正四面体的高为H,它的内切球半径为
,由此类比得:已知正四面体的高为H,它的内切球半径为 ,则
,则 .
.
对于平面上的点集 ,如果连接
,如果连接 中任意两点的线段必
中任意两点的线段必
定包含于 ,则称
,则称 为平面上的凸集。给出平面上4个
为平面上的凸集。给出平面上4个
点集的图形如右(阴影区域及其边界),其中为凸集的是
(写出其中所有凸集相应图形的序号)
对于实数x、y,定义新运算x*y=ax+by+1,其中a、b是常数,等式右边是通常的加法和乘法运算.若3*5=15,4*7=28,则1*1=_________.
在等比数列{an}中,若a10=0,则有等式
a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立.类比上述性质,相应地,在等比数列{bn}中,若b9=1,则等式______________成立 
试题篮
()