高中数学合情推理和演绎推理填空题

给出下列等式：；  
；
，
由以上等式推出一个一般结论：
对于=                        ．

设点C在线段AB上（端点除外），若C分AB的比，则得分点C的坐标公式，对于函数上任意两点，，线段AB必在弧AB上方．由图象中的点C在点C′正上方，有不等式成立．对于函数的图象上任意两点，，类比上述不等式可以得到的不等式是_________ ．

对大于或等于2的自然数 m的n 次方幂有如下分解方式：
2²＝1＋3,3²＝1＋3＋5,4²＝1＋3＋5＋7；2³＝3＋5,3³＝7＋9＋11,4³＝13＋15＋17＋19.
根据上述分解规律，若n²＝1＋3＋5＋ ＋19, m³(m∈N^*)的分解中最小的数是21，则m＋n的值为________．

已知边长分别为a、b、c的三角形ABC面积为S，内切圆O半径为r，连接OA、OB、OC，则三角形OAB、OBC、OAC的面积分别为、、，由得，类比得四面体的体积为V，四个面的面积分别为,则内切球的半径R=_________________

设函数f(x)＝ (x>0)
观察：f₁(x)＝f(x)＝，f₂(x)＝f(f₁(x))＝，f₃(x)＝f(f₂(x))＝，
f₄(x)＝f(f₃(x))＝， 根据以上事实，由归纳推理可得：
当n∈N^*且n≥2时，f_n(x)＝f(f_n－1(x))＝________.

观察分析下表中的数据：

多面体	面数（）	顶点数（)	棱数（)
三棱锥	5	6	9
五棱锥	6	6	10
立方体	6	8	12

 
猜想一般凸多面体中，所满足的等式是_________.

有一个数阵如下：记第行的第个数字为，（如），则等于        .

根据下面一组等式：
S₁＝1；
S₂＝2＋3＝5；
S₃＝4＋5＋6＝15；
S₄＝7＋8＋9＋10＝34；
S₅＝11＋12＋13＋14＋15＝65；
S₆＝16＋17＋18＋19＋20＋21＝111；
S₇＝22＋23＋24＋25＋26＋27＋28＝175；
……
可得________．

古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数，第个三角形数为.记第个边形数为（），以下列出了部分边形数中第个数的表达式：
三角形数             正方形数  
五边形数             六边形数  
可以推测的表达式，由此计算            .

已知，则       ．

观察下列等式:,…,根据上述规律,第五个等式为______________．

记，当时，观察下列等式：





……可以推测，_______.

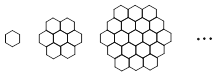
蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂
巢的截面图. 其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，
以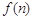表示第幅图的蜂巢总数，则=_______.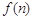

设ΔABC的三边长分别为、、，ΔABC的面积为，则ΔABC的内切圆半径为，
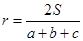将此结论类比到空间四面体：设四面体S—ABCD的四个面的面积分别为，，，，
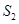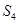体积为，则四面体的内切球半径=           ．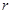

椭圆的标准方程为（），圆的标准方程，即，类比圆的面积推理得椭圆的面积         。