高中数学合情推理和演绎推理填空题

集合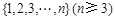中，每两个相异数作乘积，将所有这些乘积的和记为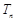，如：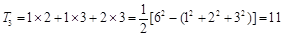
；
；

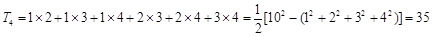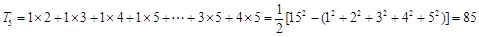
则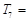          ．（写出计算结果）

将全体正整数排成一个三角形数阵：

按照以上排列的规律，第行从左向右的第3个数为           

依此类推，第个等式为                    ．

设等差数列的前n项和为则成等差数列.类比以上结论有:设等比数列的前n项积为则         ，           ，成等比数列．

由下列事实：
（a﹣b）（a+b）=a²﹣b²
（a﹣b）（a²+ab+b²）=a³﹣b³，
（a﹣b）（a³+a²b+ab²+b³）=a⁴﹣b⁴，
（a﹣b）（a⁴+a³b+a²b²+ab³+b⁴）=a⁵﹣b⁵，
可得到合理的猜想是               ．

定义表示所有满足的集合组成的有序集合对的个数．试探究，并归纳推得=_________.

在平面中，△ABC的角C的内角平分线CE分△ABC面积所成的比.将这个结论类比到空间：在三棱锥A－BCD中，平面DEC平分二面角A－CD－B且与AB交于E，则类比的结论为＝________．

如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行； ；依此类推，则
（1）按网络运作顺序第行第1个数（如第2行第1个数为2，第3行第1个数为4，）是           ；
（2）第63行从左至右的第3个数是    ．

观察下列等式2³=3+5，3³=7+9+11，4³=13+15+17+19，5³=21+23+25+27+29， ，若类似上面各式方法将m³分拆得到的等式右边最后一个数是131，则正整数m等于　_________　．

观察下列不等式



……
照此规律，第五个不等式为______________.

在Rt△ABC中，若∠C=90°，AC=b，BC=a，斜边AB上的高为h，则有结论h²=，运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为a，b，c，且三棱锥的直角顶点到底面的高为h，则有结论：          ．

如图的三角形数阵中，满足：（1）第1行的数为1；（2）第（）行首尾两数均为，其余的数都等于它肩上的两个数相加，则第行中第个数是____________.

把命题“若是正实数，则有”推广到一般情形，推广后的命题为____________.

将全体正整数排成一个三角形数阵：
1
2   3
4   5   6
7   8   9  10
按照以上排列的规律，第n 行（n ≥3）从左向右的第3 个数为         __.

观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律，第n个等式为 _________ ．