高中数学合情推理和演绎推理填空题

设a，b是两个实数，给出下列条件：
①a＋b>1；②a＋b＝2；③a＋b>2；④a²＋b²>2；⑤ab>1．
其中能推出：“a，b中至少有一个大于1”的条件是______．（填序号）

古希腊毕达哥拉斯学派的数学家研究过各种多边形数．如三角形数1,3,6,10，…，第个三角形数为．记第个边形数为，以下列出了部分边形数中第个数的表达式：
三角形数    
正方形数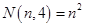     
五边形数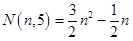     
六边形数     
……
可以推测的表达式，由此计算        ．

我们把平面内与直线垂直的非零向量称为直线的法向量，在平面直角坐标系中，利用求动点轨迹方程的方法，可以求出过点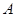，且法向量为的直线（点法式）方程为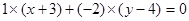，化简得．类比以上方法，在空间直角坐标系中，经过点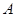，且法向量为的平面（点法式）方程为                    ．

如下图所示，坐标纸上的每个单元格的边长为，由下往上的六个点：，，，，，的横、纵坐标分别对应数列（）的前项，如下表所示：       

按如此规律下去，则        ．

如图，在等腰直角三角形中，斜边，过点作的垂线，垂足为；过点作的垂线，垂足为；过点作的垂线，垂足为；…，以此类推，设，，，…，，则________.

将全体正整数排成如图的一个三角形数阵，按照此排列规律，第10行从左向右的第5个数为                  ．

面积为的平面凸四边形的第条边的边长记为 ，此四边形内任一点到第条边的距离为，若，则；根据以上性质，体积为的三棱锥的第个面的面积为，此三棱锥内任一点到个面的距离为，若，则           ．

在平面直角坐标系上，设不等式组所表示的平面区域为，记内的整点（即横坐标和纵坐标均为整数的点）的个数为．则＝         ，经猜想可得到＝         ．

求“方程的解”有如下解题思路：设，则在上单调递减，且，所以原方程有唯一解．类比上述解题思路，方程的解为          ．

将演绎推理“函数的图像是一条直线．”恢复成完全的三段论形式，其中大前提是    ．   

把正整数按照下面的表格进行排列

1	3	6	10	15	21
2	5	9	14	20
4	8	13	19
7	12	18
11	17
16

 
则排在第6行，第4列的数是_______________；
排在第行，第列（）的数是______________

已知正三角形内切圆的半径是高的，把这个结论推广到空间正四面体，类似的结论是____________．

．甲、乙、丙三名同学中只有一人考了满分，当他们被问到谁考了满分时，回答如下．
甲说：丙没有考满分；乙说：是我考的；丙说：甲说的是真话．
事实证明：在这三名同学中，只有一人说的是假话，那么得满分的同学是     ．

计算，可以采用以下方法：
构造等式：，两边对x求导，
得，
在上式中令，得．类比上述计算方法，计算            ．

设向量 $a_k=(\cos \frac{k\pi }{6},\sin \frac{k\pi }{6}+\cos \frac{k\pi }{6})(k=0,1,2,...,12)$，则 $\underset{k=0}{\overset{11}{\sum }}(a_k·a_{k+1})$的值为.