在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的( )
| A.BC∥平面PDF |
| B.DF⊥平面PAE |
| C.平面PDE⊥平面ABC |
| D.平面PAE⊥平面ABC |
(本小题满分13分)
如图,在四棱锥 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,  ,
, 为
为 的中点,
的中点, 为
为 的中点
的中点
(Ⅰ)证明:直线
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
如图(1),在三角形ABC中,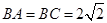 ,
,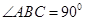 ,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.
,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.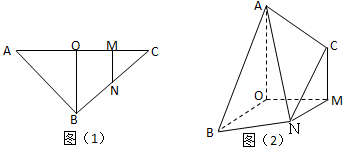
(1)求证: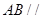 平面CMN;
平面CMN;
(2)求点M到平面CAN的距离.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
(1)求证:BC⊥A1D.
(2)求证:平面A1BC⊥平面A1BD.
(3)求三棱锥A1-BCD的体积.
如图是棱长为 的正方体的平面展开图,则在原正方体中,
的正方体的平面展开图,则在原正方体中,
① 平面
平面 ;
;
② 平面
平面 ;
;
③CN与BM成 角;
角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是____ ____。 (写出所有正确命题的序号)
(本小题满分12分)如图,在四棱锥P-ABCD中,PD^平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.

(Ⅰ)证明:PA∥平面BDE;
(Ⅱ)证明:AC^平面PBD.
试题篮
()