如图,四棱锥的底面
是平行四边形,
,
,
分别是棱
的中点.
(1)证明平面
;
(2)若二面角为
,
①证明:平面平面
.
②求直线与平面
所成角的正弦值.

如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(Ⅰ)判定AE与PD是否垂直,并说明理由;
(Ⅱ)若PA=2,求二面角E-AF-C的余弦值.
如图,四边形 为矩形,四边形
为矩形,四边形 为梯形,
为梯形, ∥
∥ ,
, ,且平面
,且平面 平面
平面 ,
, ,点
,点 为
为 的中点.
的中点.

(1)求证: ∥平面
∥平面 ;
;
(2)求三棱锥 的体积;
的体积;
(3)试判断平面 与平面
与平面 是否垂直?若垂直,请证明;若不垂直,请说明理由.
是否垂直?若垂直,请证明;若不垂直,请说明理由.
(本小题满分12分)如图,在多面体ABCDEF中,正方形 与梯形
与梯形 所在平面互相
所在平面互相
垂直,已知 ,
, ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
如图,在三棱柱 中,
中, ,
, ,
, ,
, 在底面ABC的射影为BC的中点,D为
在底面ABC的射影为BC的中点,D为 的中点.
的中点.
(1)证明: ;
;
(2)求直线 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
如图,三棱柱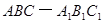 中,
中,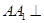 平面ABC,AB
平面ABC,AB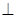 BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.
(Ⅰ)求证:MN 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC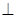 平面A1ABB1.
平面A1ABB1.
(本小题满分12分)如图,正四棱锥 的底面是边长为
的底面是边长为 的正方形,侧棱长是底面边长为
的正方形,侧棱长是底面边长为 倍,
倍, 为底面对角线的交点,
为底面对角线的交点, 为侧棱
为侧棱 上的点.
上的点.
(1)求证: ;
;
(2) 为
为 的中点,若
的中点,若 平面
平面 ,求证:
,求证: 平面
平面 .
.
(本小题满分13分)
如图5,已知点 是圆心为
是圆心为 半径为1的半圆弧上从点
半径为1的半圆弧上从点 数起的第一个三等分点,
数起的第一个三等分点, 是直径,
是直径, ,
, 平面
平面 ,点
,点 是
是 的中点.
的中点.
(1)求二面角 的余弦值.
的余弦值.
(2)求点 到平面
到平面 的距离.
的距离.
试题篮
()