 是矩形,
是矩形, ,
, ,沿
,沿 将
将 折起到
折起到 ,使平面
,使平面 平面
平面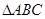 ,
, 是
是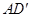 的中点,
的中点, 是
是 上的一点,给出下列结论:
上的一点,给出下列结论:
① 存在点 ,使得
,使得 平面
平面
② 存在点 ,使得
,使得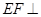 平面
平面
③ 存在点 ,使得
,使得 平面
平面
④ 存在点 ,使得
,使得 平面
平面
其中正确结论的序号是 .(写出所有正确结论的序号)
(本小题满分12分)已知四棱锥 ,侧面
,侧面 底面
底面 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面 为菱形,且
为菱形,且 .
.
(1)求证: ;
;
(2)求平面 与平面
与平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
设 为两个不重合的平面,
为两个不重合的平面, 为两条不重合的直线,给出下列四个命题:
为两条不重合的直线,给出下列四个命题:
①若 ,则
,则 ;[
;[
②若 ,则
,则 ;
;
③若 则
则 ;
;
④若 与
与 相交且不垂直,则
相交且不垂直,则 与
与 一定不垂直.
一定不垂直.
其中,所有真命题的序号是 .
设 为空间的两条直线,
为空间的两条直线, 为空间的两个平面,给出下列命题:
为空间的两个平面,给出下列命题:
①若

 ,
,

 , 则
, 则

 ;
;
②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则

 ;
;
③若

 ,
,

 ,则
,则

 ;
;
④若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则

 ;
;
上述命题中,其中假命题的序号是 .
在空间中,用a,b,c表示三条不同的直线,γ表示平面,给出下列四个命题:
(1)若a∥b,b∥c,则a∥c;
(2)若a⊥b,b⊥c,则a⊥c;
(3)若a∥γ,b∥γ,则a∥b;
(4)若a⊥γ,b⊥γ,则a∥b.
其中真命题的序号为 .
在直三棱柱 中,若
中,若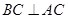 ,
, ,
, ,
, 为
为 中点,点
中点,点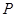
为 中点,
中点, 在线段
在线段 上,且
上,且 ,则
,则 的长度为________ .
的长度为________ .
试题篮
()