从某批产品中,有放回地抽取产品2次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率为0.84.
(Ⅰ)求事件“从该批产品中任取1件产品,取到的是二等品”的概率p;
(Ⅱ)若从20件该产品中任意抽取3件,求事件B:“取出的3件产品中至少有一件二等品”的概率 .
.
两个人射击,甲射击一次中靶概率是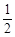 ,乙射击一次中靶概率是
,乙射击一次中靶概率是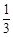 ,
,
(Ⅰ)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(Ⅱ)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(Ⅲ)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过
检测,每一件二等品通过检测的概率为 .现有10件产品,其中6件是一等品,4件是二等
.现有10件产品,其中6件是一等品,4件是二等
品.
(Ⅰ) 随机选取1件产品,求能够通过检测的概率;
(Ⅱ) 随机选取3件产品,其中一等品的件数记为 ,求
,求 的分布列;
的分布列;
(Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.
在一个有奖问答的电视节目中,参赛选手顺序回答 三个问题,答对各个问题所获奖金(单位:元)对应如下表:
三个问题,答对各个问题所获奖金(单位:元)对应如下表:
 |
 |
 |
 |
 |
 |
当一个问题回答正确后,选手可选择继续回答下一个问题,也可选择放弃.若选择放弃,选手将获得答对问题的累计奖金,答题结束;若有任何一个问题回答错误,则全部奖金归零,答题结束.设一名选手能正确回答 的概率分别为
的概率分别为 ,正确回答一个问题后,选择继续回答下一个问题的概率均为
,正确回答一个问题后,选择继续回答下一个问题的概率均为 ,且各个
,且各个 问题回答正确与否互不影响.
问题回答正确与否互不影响.
(Ⅰ)按照答题规则,求该选手 回答正确但所得奖金为零的概率;
回答正确但所得奖金为零的概率;
(Ⅱ)设该选手所获奖金总数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
一射击测试每人射击二次,甲每击中目标一次记10分,没有击中记0分,每次击中目标的概率为 ;乙每击中目标一次记20分,没有击中记0分,每次击中目标的概率为
;乙每击中目标一次记20分,没有击中记0分,每次击中目标的概率为 .
.
(Ⅰ)求甲得10分的概率;
(Ⅱ)求甲乙两人得分相同的概率.
六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。
①求某个学生不被淘汰的概率。
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的概率。
的概率。
老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1)抽到他能背诵的课文的数量的分布列;
(2)他能及格的概率.
第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语。
(I)根据以上数据完成以下2X2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?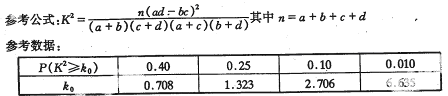
(II)若从会俄语的记者中随机抽取3人成立一个小组,则小组中既有男又有女的概率是多少?
(III)若从14名女记者中随机抽取2人担任翻译工作,记会俄语的人数为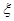 ,求
,求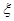 的期望。
的期望。
某工厂在试验阶段大量生产一种零件.这种零件有A,B两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为5/12,至少一项技术指标达标的概率为11/12.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?
(3)任意依次抽取该种零件4个,设ξ表示其中合格品的个数,求Eξ与Dξ.
一台仪器每启动一次都随机地出现一个5位二进制数
| A1 |
A2 |
A3 |
A4 |
A5 |
A=
其中A1=1,Ak(k=2,3,4,5)为0的概率为 ,为1的概率为
,为1的概率为 .例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
.例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
(1)P(m="3) " (2)P(m≤3)
假设每一架飞机引擎在飞行中故障率为1–p,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行,则对于多大的p而言,4引擎飞机比2引擎飞机更为安全?
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进行第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品的合格率依次为 ,
, ,
, .经过第二次烧制后,甲、乙、丙三件产品的合格率均为
.经过第二次烧制后,甲、乙、丙三件产品的合格率均为 .
.
(Ⅰ)求第一次烧制后恰有一件产品合格的概率;
(Ⅱ)求经过前后两次烧制后三件产品均合格的概率.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
( I ) 求这次铅球测试成绩合格的人数;
(II)用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记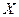 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求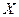 的数学期望和方差.
的数学期望和方差.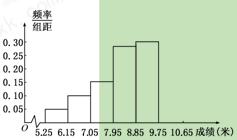
试题篮
()