高中数学正交试验设计方法解答题

一个袋中有1个白球和4个黑球，每次从中任取一个球，每次所取的球放回，直到取得白球为止，但摸球次数不超过5次，求取球次数的分布列

已知射手甲射击一次，命中9环（含9环）以上的概率为0.56，命中8环的概率为0.22，命中7环的概率为0.12．
①求甲射击一次，命中不足8环的概率.
②求甲射击一次，至少命中7环的概率.

有甲，乙两个盒子，甲盒中装有2个小球，乙盒中装有3个小球，每次随机选取一个盒子并从中取出一个小球
（1）当甲盒中的球被取完时，求乙盒中恰剩下1个球的概率；
（2）当第一次取完一个盒子中的球时，另一个盒子恰剩下个球，求的分布列及期望。

某装置由两套系统M,N组成，只要有一套系统工作正常，该装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成（如图所示已知T1,T2,T3正常工作的概率都是，且T1,T2,T3能否正常工作相互独立.(注：对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)

(I )分别求系统M,N正常工作的概率；
(II)设该装I中两套系统正常工作的套数为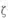，求的分布列和期望.

（本题12分）已知某种从太空带回的植物种子每粒成功发芽的概率都为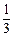，某植物研究所分两个小组分别独立开展该种子的发芽实验，每次实验种一粒种子，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．
(1) 第一小组做了三次实验，求实验成功的平均次数；
(2) 第二小组连续进行实验，求实验首次成功时所需的实验次数的期望；
(3)两个小组分别进行2次试验，求至少有2次实验成功的概率．

一场篮球比赛到了最后5分钟，甲队比乙队少得5分。如果甲队全投3分球，则有8次投篮机会。如果甲队全投2分球，则有3次投篮机会。假设甲队队员投3分球的命中率均为0.6，投2分球的命中率均为0 .8，并且甲队加强防守，不给乙队投篮机会．问全投3分球与全投2分球这两种方案中选择哪一种甲队获胜的概率较大？

甲、乙、丙三人进行乒乓球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为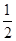，各局比赛的结果相互独立，第1局甲当裁判．
（1）求第4局甲当裁判的概率；
（2）用X表示前4局中乙当裁判的次数，求X的分布列和数学期望．

如果在一次试验中，某事件A发生的概率为p，那么在n次独立重复试验中，求事件A发生偶数次的概率．

为了解某市市民对政府出台楼市限购令的态度，在该市随机抽取了50名市民进行调查，他们月收入（单位：百元）的频数分布及对楼市限购令的赞成人数如下表：

月收入		[25，35）	[35，45）
频数	5	10	15	10	5	5
赞成人数	4	8	8	5	2	1

将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收人族”。
（Ⅰ）根据已知条件完成下面的2×2列联表，有多大的把握认为赞不赞成楼市限购令与收入高低有关？
已知：，
当<2.706时，没有充分的证据判定赞不赞成楼市限购令与收入高低有关；
当>2.706时，有90％的把握判定赞不赞成楼市限购令与收入高低有关；
当>3.841时，有95％的把握判定赞不赞成楼市限购令与收入高低有关；
当>6.635时，有99％的把握判定赞不赞成楼市限购令与收入高低有关。

	非高收入族	高收入族	总计
赞成
不赞成
总计

（Ⅱ）现从月收入在[55，65）的人群中随机抽取两人，求所抽取的两人中至少一人赞成楼市限购令的概率。

（本小题满分12分）已知高二年级的某6名学生，独立回答某类问题时答对的概率都是0.5，而将这6名同学平均分为甲、乙、丙3个小组后，每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7，若各个同学或各个小组回答问题时都是相互独立的．
（Ⅰ）这6名同学平均分成3组，共有分法多少种？
（Ⅱ）若分组后，3个小组中恰有2组能答对此类问题的概率是多少？
（Ⅲ）若要求独立回答，则这6名学生中至多有4人能答对此类问题的概率是多少？

某中学经市批准建设分校，工程从2010年底开工到2013年底完工，分三期完成，经过初步招标淘汰后，确定由甲、乙两建筑公司承建，且每期工程由两公司之一独立完成，必须在建完前一期工程后再建后一期工程，已知甲公司获得第一期，第二期，第三期工程承包权的概率分别是，，．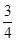
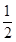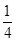(I)求甲乙两公司均至少获得l期工程的概率；
(II)求甲公司获得的工程期数的分布列和数学期望E(X)．

5名工人独立地工作，假定每名工人在1小时内平均12分钟需要电力（即任一时刻需要电力的概率为12/60）
（1）设X为某一时刻需要电力的工人数，求 X的分布列及期望；
（2）如果同一时刻最多能提供3名工人需要的电力，求电力超负荷的概率，并解释实际意义．

.在集合内任取一个元素，能使代数式的概率是多少？

某地举行篮球比赛，其中男子篮球总决赛在雄风队与豪杰队之间角逐，采用七局四胜制，若有一队胜4场，由此队获胜且结束比赛，因而队实力非常接近，在每场比赛中两队获胜是等可能的。据以往资料统计，每场比赛组织者可获门票收入5万元，两队决出胜负后，问：
（1）求组织者在此次决赛中获门票收入为20万元的概率。
（2）求组织者在此次决赛中获门票收入不少于30万元的概率。
（1）门票收入20万无，必须比赛四场，且能决出胜负

某足球俱乐部2013年10月份安排4次体能测试，规定：按顺序测试，一旦测试合格就不必参加以后的测试，否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为的等差数列，他第一次测试合格的概率不超过，且他直到第二次测试才合格的概率为。
（Ⅰ）求小李第一次参加测试就合格的概率P₁；
（2）求小李10月份参加测试的次数x的分布列和数学期望。