高中数学正交试验设计方法解答题

某次考试共有8道选择题，每道选择题有四个选项，只有一道是正确的，评分标准为：“选对得5分，不选或选错得0分。”某考生已确定有5道题的答案是正确的，其余3道题中，有一道题可以判断出两个选项是错误的，有一道题可以判断出一个选项是错误的，还有一道是乱猜的，试求该考生
（1）得40分的概率；
（2）所得分数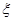的分布及期望．

某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间（单位：分钟）进行了统计，如下表．若视频率为概率，请用有关知识解决下列问题．

病症及代号	普通病症	复诊病症	常见病症	疑难病症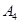	特殊病症
人数	100	300	200	300	100
每人就诊时间（单位：分钟）	3	4	5	6	7

用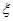表示某病人诊断所需时间，求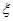的数学期望．
并以此估计专家一上午（按3小时计算）可诊断多少病人；
某病人按序号排在第三号就诊，设他等待的时间为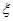，求；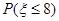
求专家诊断完三个病人恰好用了一刻钟的概率．

北京的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率; 
(Ⅱ) 该考生所得分数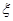的分布列及数学期望.

如果在一次试验中，某事件A发生的概率为p，那么在n次独立重复试验中，求事件A发生偶数次的概率．

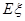高三年级有3名男生和1名女生为了报某所大学，事先进行了多方详细咨询，并根据自己的高考成绩情况，最终估计这3名男生报此所大学的概率都是，这1名女生报此所大学的概率是．且这4人报此所大学互不影响。
（Ⅰ）求上述4名学生中报这所大学的人数中男生和女生人数相等的概率；
（Ⅱ）在报考某所大学的上述4名学生中，记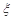为报这所大学的男生和女生人数的和，试求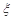的分布列和数学期望．

某地举行篮球比赛，其中男子篮球总决赛在雄风队与豪杰队之间角逐，采用七局四胜制，若有一队胜4场，由此队获胜且结束比赛，因而队实力非常接近，在每场比赛中两队获胜是等可能的。据以往资料统计，每场比赛组织者可获门票收入5万元，两队决出胜负后，问：
（1）求组织者在此次决赛中获门票收入为20万元的概率。
（2）求组织者在此次决赛中获门票收入不少于30万元的概率。
（1）门票收入20万无，必须比赛四场，且能决出胜负

某射手击中目标的概率为0.8，每次射击的结果相互独立，现射击10次，问他最有可能射中几次？

2011.年广州亚运会的一组志愿者全部通晓中文，并且每个志愿者还都通晓英语、日语和韩语中的一种（但无人通晓两种外语).已知从中任抽一人，其通晓中文和英语的概率为，通晓中文和日语的概率为.若通晓中文和韩语的人数不超过3人.
(I )求这组志愿者的人数；
(II)现从这组志愿者中选出通晓英语的志愿者1名，通晓韩语的志愿者1名，若甲通晓英语，乙通晓韩语，求甲和乙不全被选中的概率.

.在集合内任取一个元素，能使代数式的概率是多少？

（本题12分）已知某种从太空带回的植物种子每粒成功发芽的概率都为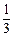，某植物研究所分两个小组分别独立开展该种子的发芽实验，每次实验种一粒种子，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．
(1) 第一小组做了三次实验，求实验成功的平均次数；
(2) 第二小组连续进行实验，求实验首次成功时所需的实验次数的期望；
(3)两个小组分别进行2次试验，求至少有2次实验成功的概率．

“低碳经济”是促进社会可持续发展的推进器.某企业现有100万元资金可用于投资，如果投资“传统型”经济项目，一年后可能获利20%，可能损失10%,也可能不赔不赚，这三种情况发生的概率分别为；如果投资“低碳型”经济项目，一年后可能获利30%,也
可能损失20%，这两种情况发生的概率分别为a和n (其中a + b =1 )如果把100万元投资“传统型”经济项目，用表示投资收益（投资收益=回收资金一投资资金)，求的概率分布及均值（数学期望）；(II)如果把100万元投资“低碳型”经济项目，预测其投资收益均值会不低于投资“传统型”经济项目的投资收益均值，求a的取值范围

甲乙两人各有相同的小球10个，在每人的10个小球中都有5个标有数字1，3个标有数字2，2个标有数字3。两人同时分别从自己的小球中任意抽取1个，规定：若抽取的两个小球上的数字相同，则甲获胜，否则乙获胜，求乙获胜的概率。

某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立）．
(１)求至少3人同时上网的概率；
(２)至少几人同时上网的概率小于0.3？

一场篮球比赛到了最后5分钟，甲队比乙队少得5分。如果甲队全投3分球，则有8次投篮机会。如果甲队全投2分球，则有3次投篮机会。假设甲队队员投3分球的命中率均为0.6，投2分球的命中率均为0 .8，并且甲队加强防守，不给乙队投篮机会．问全投3分球与全投2分球这两种方案中选择哪一种甲队获胜的概率较大？

某装置由两套系统M,N组成，只要有一套系统工作正常，该装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成（如图所示已知T1,T2,T3正常工作的概率都是，且T1,T2,T3能否正常工作相互独立.(注：对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)

(I )分别求系统M,N正常工作的概率；
(II)设该装I中两套系统正常工作的套数为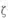，求的分布列和期望.