如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的弧,曲线CA1A2A3称为螺旋线旋转一圈.然后又以A为圆心AA3为半径画弧,这样画到第n圈,则所得螺旋线的长度 _____________.(用π表示即可)
_____________.(用π表示即可)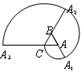
如图,圆 内有一点
内有一点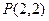 ,过点
,过点 作直线
作直线 交圆于
交圆于 两点.(1)当直线
两点.(1)当直线 经过圆心
经过圆心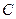 时,求直线
时,求直线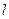 的方程;(2)当弦
的方程;(2)当弦 被点
被点 平分时,写出直线
平分时,写出直线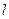 方程;(3)当直线
方程;(3)当直线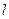 倾斜角为
倾斜角为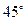 时,求
时,求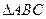 的面积.
的面积.

已知动圆过定点P(1,0),且与定直线 相切,点C在
相切,点C在 上.
上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为- 的直线与曲线M相交于A、B两点,
的直线与曲线M相交于A、B两点,
①求线段AB的长;
②问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?
?
存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知圆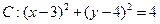 和直线
和直线 ,直线
,直线 ,
, 都经过圆C外
都经过圆C外
定点A(1,0).
(Ⅰ)若直线 与圆C相切,求直线
与圆C相切,求直线 的方程;
的方程;
(Ⅱ)若直线 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: 为定值.
为定值.
如下图所示,在直角坐标系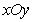 中,射线
中,射线 在第一象限,且与
在第一象限,且与 轴的正半轴成定角
轴的正半轴成定角 ,动点
,动点 在射线
在射线 上运动,动点
上运动,动点 在
在 轴的正半轴上运动,
轴的正半轴上运动, 的面积为
的面积为 .
.
(Ⅰ)求线段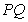 中点
中点 的轨迹
的轨迹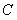 的方程;
的方程;
(Ⅱ) 是曲线
是曲线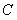 上的动点,
上的动点,  到
到 轴的距离之和为
轴的距离之和为 ,
,
设 为
为 到
到 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数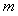 ,
,
使 恒成立?若存在,求出这个
恒成立?若存在,求出这个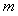 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
方程 的两个根可分别作为( ).
的两个根可分别作为( ).
| A.一椭圆和一双曲线的离心率 | B.一椭圆和一抛物线的离心率 |
| C.两椭圆的离心率 | D.两双曲线的离心率 |
试题篮
()