放射性元素由于 不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯1
不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯1 37的衰变过程中,其含
37的衰变过程中,其含 量
量 (单位:太贝克)与时间
(单位:太贝克)与时间 (单位:年)满足函数关系:
(单位:年)满足函数关系:
 ,其中
,其中 为
为 时铯137的含量,已知
时铯137的含量,已知 时,铯137的含量的变化率是
时,铯137的含量的变化率是 (太贝克/年),则
(太贝克/年),则 太贝克.
太贝克.
四人赛跑,假设其跑过的路程与时间的函数关系分别是 ,
, ,
, ,
, ,若让他们一直跑下去,则最终跑在最前面的人具有的函数关系是( )
,若让他们一直跑下去,则最终跑在最前面的人具有的函数关系是( )
A. |
B. |
C. |
D. |
(本题满分14分,第1小题满分4分,第2小题满分4分,第3小题满分6分)
设函数 ,
,
(1)求 的反函数
的反函数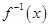 ;
;
(2)判断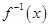 的单调性,不必证明;
的单调性,不必证明;
(3)令 ,当
,当

 ,
, 时,
时,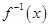 在
在 上的值域是
上的值域是 ,求
,求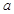 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求满足
时,求满足 的
的 的取值范围;
的取值范围;
(2)若 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 的解析式,判断其在R上的单调性并加以证明.
的解析式,判断其在R上的单调性并加以证明.
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
试题篮
()