已知 ,函数
,函数 的零点分别为
的零点分别为 ,函数
,函数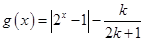 的零点分别为
的零点分别为 ,则
,则 的最小值为( )
的最小值为( )
A. |
B.2 | C. |
D.1 |
在下列区间中,函数f(x)=ex+4x﹣3的零点所在的区间为( )
A.(﹣ ,0) ,0) |
B.(0, ) ) |
C.( , , ) ) |
D.( , , ) ) |
已知函数 的定义域为
的定义域为 ,并满足(1)对于一切实数
,并满足(1)对于一切实数 ,都有
,都有 ;
;
(2)对任意的 ; (3)
; (3) ;
;
利用以上信息求解下列问题:
(1)求 ;
;
(2)证明 ;
;
(3)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
| A.{-2,0,2} | B.(1,+∞) | C.{k|k>e} | D.{k|k2>1} |
设函数f(x)=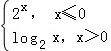 ,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
| A.1 | B.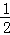 |
C. |
D.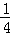 |
已知直线y=mx与函数 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.( ,4) ,4) |
B.( ,+∞) ,+∞) |
C.( ,5) ,5) |
D.( , , ) ) |
试题篮
()